記事の書き方にもだんだん慣れてきました。これからはもう少し見やすさも意識して書きたいと思います!
さて、今回は閉空間(直方体)の共振周波数と音響モードを求めたいと思います。基本的に理論式などは教科書などの文献を参考にしているので、諸元を記載したいと思います。本記事で参考にしているのは下記文献なので、詳しい導出過程は下記文献でご確認お願いします。

$$
{k_n}^2 = \frac{{ω_n}^2}{{c_o}^2}=[\frac{n_1\pi}{L_1}]^2+[\frac{n_2\pi}{L_2}]^2+[\frac{n_3\pi}{L_3}]^2
$$
参考文献ではkn^2が固有値と述べられています(これが固有値なのかの議論はここではしません。)
wnは固有角振動数、nはモード次数です。(モード次数というより、「節の数」だと思ってください。)
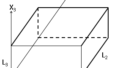
この直方体の壁が剛体(反射率が1)のときモードベクトルψnは下記のように表すことができます。
$$
{\psi_n}=\sqrt{\epsilon_1 \epsilon_2 \epsilon_3} \ cos{\frac{n_1\pi x_1}{L_1}} \ cos{\frac{n_2\pi x_2}{L_2}} \ cos{\frac{n_3\pi x_3}{L_3}}
$$
ここでεは正規化係数であり、上記式では下記関係が成立します。
$$
L_1 > L_2 > L_3
$$
if \(n_{axis} = 0\) , \( \epsilon_{axis} = 1 \)
elseif \(n_1=n_2=n_3 = 0 \)、\( \epsilon_{axis} = 0 \)
else \(n_{axis} \neq 0 \), \( \epsilon_{axis} = 2 \)
一連の式展開のプログラムを下に添付しましたので、ご確認ください。
振動のモード法で説明したのと同様に、音響についてもモードベクトルの重ね合わせで音場を表現できます。そのため上記ψが計算できれば、音場を表現することができます。また、入力点から応答点(受音点)までの周波数応答関数(Frequency Response Function:FRF)を計算することができるようになります。
ここらへんの説明は次回したいと思います。
今回はこのへんでGood luck
メインコード(実行コード)
clear all % % % % size of rectangular parallelopiped L1=3; L2=2; L3=1; V=L1*L2*L3; % % % % Constant value co=344; rho=1.205; % % % % modal numbers n_max=100; Combi=combinator(n_max,3,'p','r')-1; % % % % setting max frequency f_max=10*10^3; % % % % xi xi=[0.5 0.5 0.5]; % % % % function wn [wn]=angular_frequency(Combi,L1,L2,L3,co); % % % % function psi psi(modal number , x_number) [psi]=Psi(xi_front,Combi,L1,L2,L3); [wn,I] =sortrows(wn);
function [wn]=angular_frequency(Combi,L1,L2,L3,co)
wn=zeros(size(Combi,1),1);
for n=1:size(Combi,1)
wn(n,1)=.....
co*sqrt(....
(Combi(n,1)*pi/L1)^2.....
+ (Combi(n,2)*pi/L2)^2.....
+ (Combi(n,3)*pi/L3)^2.....
);
end
end
function [psix]=Psi(xi,Combi,L1,L2,L3)
psix=zeros(size(Combi,1),size(xi,1));
for nx=1:size(xi,1)
for n=1:size(Combi,1)
if Combi(n,1)==0
e1=1;
else
e1=2;
end
if Combi(n,2)==0
e2=1;
else
e2=2;
end
if Combi(n,3)==0
e3=1;
else
e3=2;
end
psix( n , nx )=.....
sqrt(e1*e2*e3)*....
cos(Combi(n,1)*pi* xi(nx,1)/L1)*....
cos(Combi(n,2)*pi* xi(nx,2)/L2)*....
cos(Combi(n,3)*pi* xi(nx,3)/L3);
end
end
end
MATLAB centralより
function [A] = combinator(N,K,s1,s2)
%COMBINATOR Perform basic permutation and combination samplings.
% COMBINATOR will return one of 4 different samplings on the set 1:N,
% taken K at a time. These samplings are given as follows:
%
% PERMUTATIONS WITH REPETITION/REPLACEMENT
% COMBINATOR(N,K,'p','r') -- N >= 1, K >= 0
% PERMUTATIONS WITHOUT REPETITION/REPLACEMENT
% COMBINATOR(N,K,'p') -- N >= 1, N >= K >= 0
% COMBINATIONS WITH REPETITION/REPLACEMENT
% COMBINATOR(N,K,'c','r') -- N >= 1, K >= 0
% COMBINATIONS WITHOUT REPETITION/REPLACEMENT
% COMBINATOR(N,K,'c') -- N >= 1, N >= K >= 0
%
% Example:
%
% To see the subset relationships, do this:
% combinator(4,2,'p','r') % Permutations with repetition
% combinator(4,2,'p') % Permutations without repetition
% combinator(4,2,'c','r') % Combinations with repetition
% combinator(4,2,'c') % Combinations without repetition
%
%
% If it is desired to use a set other than 1:N, simply use the output from
% COMBINATOR as an index into the set of interest. For example:
%
% MySet = ['a' 'b' 'c' 'd'];
% MySetperms = combinator(length(MySet),3,'p','r'); % Take 3 at a time.
% MySetperms = MySet(MySetperms)
%
%
% Class support for input N:
% float: double, single
% integers: int8,int16,int32
%
%
% Notes:
% All of these algorithms have the potential to create VERY large outputs.
% In each subfunction there is an anonymous function which can be used to
% calculate the number of row which will appear in the output. If a rather
% large output is expected, consider using an integer class to conserve
% memory. For example:
%
% M = combinator(int8(30),3,'p','r'); % NOT uint8(30)
%
% will take up 1/8 the memory as passing the 30 as a double. See the note
% below on using the MEX-File.
%
% To make your own code easier to read, the fourth argument can be any
% string. If the string begins with an 'r' (or 'R'), the function
% will be called with the replacement/repetition algorithm. If not, the
% string will be ignored.
% For instance, you could use: 'No replacement', or 'Repetition allowed'
% If only two inputs are used, the function will assume 'p','r'.
% The third argument must begin with either a 'p' or a 'c' but can be any
% string beyond that.
%
% The permutations with repetitions algorithm uses cumsum. So does the
% combinations without repetition algorithm for the special case of K=2.
% Unfortunately, MATLAB does not allow cumsum to work with integer classes.
% Thus a subfunction has been placed at the end for the case when these
% classes are passed. The subfunction will automatically pass the
% necessary matrix to the built-in cumsum when a single or double is used.
% When an integer class is used, the subfunction first looks to see if the
% accompanying MEX-File (cumsumall.cpp) has been compiled. If not,
% then a MATLAB For loop is used to perform the cumsumming. This is
% VERY slow! Therefore it is recommended to compile the MEX-File when
% using integer classes.
% The MEX-File was tested by the author using the Borland 5.5 C++ compiler.
%
% See also, perms, nchoosek, npermutek (on the FEX)
%
% Author: Matt Fig
% Contact: popkenai@yahoo.com
% Date: 5/30/2009
%
% Reference: http://mathworld.wolfram.com/BallPicking.html
ng = nargin;
if ng == 2
s1 = 'p';
s2 = 'r';
elseif ng == 3
s2 = 'n';
elseif ng ~= 4
error('Only 2, 3 or 4 inputs are allowed. See help.')
end
if isempty(N) || K == 0
A = [];
return
elseif numel(N)~=1 || N<=0 || ~isreal(N) || floor(N) ~= N
error('N should be one real, positive integer. See help.')
elseif numel(K)~=1 || K<0 || ~isreal(K) || floor(K) ~= K
error('K should be one real non-negative integer. See help.')
end
STR = lower(s1(1)); % We are only interested in the first letter.
if ~strcmpi(s2(1),'r')
STR = [STR,'n'];
else
STR = [STR,'r'];
end
try
switch STR
case 'pr'
A = perms_rep(N,K); % strings
case 'pn'
A = perms_no_rep(N,K); % permutations
case 'cr'
A = combs_rep(N,K); % multichoose
case 'cn'
A = combs_no_rep(N,K); % choose
otherwise
error('Unknown option passed. See help')
end
catch
rethrow(lasterror) % Throw error from here, not subfunction.
% The only error thrown should be K>N for non-replacement calls.
end
function PR = perms_rep(N,K)
% This is (basically) the same as npermutek found on the FEX. It is the
% fastest way to calculate these (in MATLAB) that I know.
% pr = @(N,K) N^K; Number of rows.
% A speed comparison could be made with COMBN.m, found on the FEX. This
% is an excellent code which uses ndgrid. COMBN is written by Jos.
%
% % All timings represent the best of 4 consecutive runs.
% % All timings shown in subfunction notes used this configuration:
% % 2007a 64-bit, Intel Xeon, win xp 64, 16 GB RAM
% tic,Tc = combinator(single(9),7,'p','r');toc
% %Elapsed time is 0.199397 seconds. Allow Ctrl+T+C+R on block
% tic,Tj = combn(single(1:9),7);toc
% %Elapsed time is 0.934780 seconds.
% isequal(Tc,Tj) % Yes
if N==1
PR = ones(1,K,class(N));
return
elseif K==1
PR = (1:N).';
return
end
CN = class(N);
M = double(N); % Single will give us trouble on indexing.
L = M^K; % This is the number of rows the outputs will have.
PR = zeros(L,K,CN); % Preallocation.
D = ones(1,N-1,CN); % Use this for cumsumming later.
LD = M-1; % See comment on N.
VL = [-(N-1) D].'; % These values will be put into PR.
% Now start building the matrix.
TMP = VL(:,ones(L/M,1,CN)); % Instead of repmatting.
PR(:,K) = TMP(:); % We don't need to do two these in loop.
PR(1:M^(K-1):L,1) = VL; % The first column is the simplest.
% Here we have to build the cols of PR the rest of the way.
for ii = K-1:-1:2
ROWS = 1:M^(ii-1):L; % Indices into the rows for this col.
TMP = VL(:,ones(length(ROWS)/(LD+1),1,CN)); % Match dimension.
PR(ROWS,K-ii+1) = TMP(:); % Build it up, insert values.
end
PR(1,:) = 1; % For proper cumsumming.
PR = cumsum2(PR); % This is the time hog.
function PN = perms_no_rep(N,K)
% Subfunction: permutations without replacement.
% Uses the algorithm in combs_no_rep as a basis, then permutes each row.
% pn = @(N,K) prod(1:N)/(prod(1:(N-K))); Number of rows.
if N==K
PN = perms_loop(N); % Call helper function.
% [id,id] = sort(PN(:,1)); %#ok Not nec., uncomment for nice order.
% PN = PN(id,:); % Return values.
return
elseif K==1
PN = (1:N).'; % Easy case.
return
end
if K>N % Since there is no replacement, this cannot happen.
error(['When no repetitions are allowed, '...
'K must be less than or equal to N'])
end
M = double(N); % Single will give us trouble on indexing.
WV = 1:K; % Working vector.
lim = K; % Sets the limit for working index.
inc = 1; % Controls which element of WV is being worked on.
BC = prod(M-K+1:M); % Pre-allocation of return arg.
BC1 = BC / ( prod(1:K)); % Number of comb blocks.
PN = zeros(round(BC),K,class(N));
L = prod(1:K) ; % To get the size of the blocks.
cnt = 1+L;
P = perms_loop(K); % Only need to use this once.
PN(1:(1+L-1),:) = WV(P); % The first row.
for ii = 2:(BC1 - 1);
if logical((inc+lim)-N) % The logical is nec. for class single(?)
stp = inc; % This is where the for loop below stops.
flg = 0; % Used for resetting inc.
else
stp = 1;
flg = 1;
end
for jj = 1:stp
WV(K + jj - inc) = lim + jj; % Faster than a vector assignment!
end
PN(cnt:(cnt+L-1),:) = WV(P); % Assign block.
cnt = cnt + L; % Increment base index.
inc = inc*flg + 1; % Increment the counter.
lim = WV(K - inc + 1 ); % lim for next run.
end
V = (N-K+1):N; % Final vector.
PN(cnt:(cnt+L-1),:) = V(P); % Fill final block.
% The sorting below is NOT necessary. If you prefer this nice
% order, the next two lines can be un-commented.
% [id,id] = sort(PN(:,1)); %#ok This is not necessary!
% PN = PN(id,:); % Return values.
function P = perms_loop(N)
% Helper function to perms_no_rep. This is basically the same as the
% MATLAB function perms. It has been un-recursed for a runtime of around
% half the recursive version found in perms.m For example:
%
% tic,Tp = perms(1:9);toc
% %Elapsed time is 0.222111 seconds. Allow Ctrl+T+C+R on block
% tic,Tc = combinator(9,9,'p');toc
% %Elapsed time is 0.143219 seconds.
% isequal(Tc,Tp) % Yes
M = double(N); % Single will give us trouble on indexing.
P = 1; % Initializer.
G = cumprod(1:(M-1)); % Holds the sizes of P.
CN = class(N);
for n = 2:M
q = P;
m = G(n-1);
P = zeros(n*m,n,CN);
P(1:m, 1) = n;
P(1:m, 2:n) = q;
a = m + 1;
for ii = n-1:-1:1,
t = q;
t(t == ii) = n;
b = a + m - 1;
P(a:b, 1) = ii;
P(a:b, 2:n) = t;
a = b + 1;
end
end
function CR = combs_rep(N,K)
% Subfunction multichoose: combinations with replacement.
% cr = @(N,K) prod((N):(N+K-1))/(prod(1:K)); Number of rows.
M = double(N); % Single will give us trouble on indexing.
WV = ones(1,K,class(N)); % This is the working vector.
mch = prod((M:(M+K-1)) ./ (1:K)); % Pre-allocation.
CR = ones(round(mch),K,class(N));
for ii = 2:mch
if WV(K) == N
cnt = K-1; % Work backwards in WV.
while WV(cnt) == N
cnt = cnt-1; % Work backwards in WV.
end
WV(cnt:K) = WV(cnt) + 1; % Fill forward.
else
WV(K) = WV(K)+1; % Keep working in this group.
end
CR(ii,:) = WV;
end
function CN = combs_no_rep(N,K)
% Subfunction choose: combinations w/o replacement.
% cn = @(N,K) prod(N-K+1:N)/(prod(1:K)); Number of rows.
% Same output as the MATLAB function nchoosek(1:N,K), but often faster for
% larger N.
% For example:
%
% tic,Tn = nchoosek(1:17,8);toc
% %Elapsed time is 0.430216 seconds. Allow Ctrl+T+C+R on block
% tic,Tc = combinator(17,8,'c');toc
% %Elapsed time is 0.024438 seconds.
% isequal(Tc,Tn) % Yes
if K>N
error(['When no repetitions are allowed, '...
'K must be less than or equal to N'])
end
M = double(N); % Single will give us trouble on indexing.
if K == 1
CN =(1:N).'; % These are simple cases.
return
elseif K == N
CN = (1:N);
return
elseif K==2 && N>2 % This is an easy case to do quickly.
BC = (M-1)*M / 2;
id1 = cumsum2((M-1):-1:2)+1;
CN = zeros(BC,2,class(N));
CN(:,2) = 1;
CN(1,:) = [1 2];
CN(id1,1) = 1;
CN(id1,2) = -((N-3):-1:0);
CN = cumsum2(CN);
return
end
WV = 1:K; % Working vector.
lim = K; % Sets the limit for working index.
inc = 1; % Controls which element of WV is being worked on.
BC = prod(M-K+1:M) / (prod(1:K)); % Pre-allocation.
CN = zeros(round(BC),K,class(N));
CN(1,:) = WV; % The first row.
for ii = 2:(BC - 1);
if logical((inc+lim)-N) % The logical is nec. for class single(?)
stp = inc; % This is where the for loop below stops.
flg = 0; % Used for resetting inc.
else
stp = 1;
flg = 1;
end
for jj = 1:stp
WV(K + jj - inc) = lim + jj; % Faster than a vector assignment.
end
CN(ii,:) = WV; % Make assignment.
inc = inc*flg + 1; % Increment the counter.
lim = WV(K - inc + 1 ); % lim for next run.
end
CN(ii+1,:) = (N-K+1):N;
function A = cumsum2(A)
%CUMSUM2, works with integer classes.
% Duplicates the action of cumsum, but for integer classes.
% If Matlab ever allows cumsum to work for integer classes, we can remove
% this.
if isfloat(A)
A = cumsum(A); % For single and double, use built-in.
return
else
try
A = cumsumall(A); % User has the MEX-File ready?
catch
warning('Cumsumming by loop. MEX cumsumall.cpp for speed.') %#ok
for ii = 2:size(A,1)
A(ii,:) = A(ii,:) + A(ii-1,:); % User likes it slow.
end
end
end

コメント