はじめに
振動工学やモード解析をご存じの方であれば、一度は読んだことがあると言われているバイブル的な書籍「モード解析入門」について再復習しております。今回はモード解析入門の2.5.5項の「基礎への伝達力」のP.60から復習します。なお、振動工学の参考書はどの本も似たり寄ったりで内容が重複しています。例えば、「実用モード解析入門」は長松先生の息子さんが著者ということもあり、重複している部分が多いです。
各参考書で重複している部分は本記事で大まかに理解できると思いますので、他の参考書から本記事へアクセスした場合も最後まで読んでいただけると幸いです。

防振ゴムとは
モード解析入門の解説をする前に「防振ゴム」について説明します。
防振ゴムはほぼすべての機械の振動絶縁(防振)に使われています。みなさんに身近な例としては、洗濯機や乾燥機の下(機械の足と床の間)にゴムが使われています。このゴムによって、床に伝わる振動が低減(絶縁)されます。他にも、モーターやエンジンなども防振ゴム付きのねじなどでマウントされています。家電用の後付けの防振ゴムはホームセンターなんかでも売られていますね。

図 乾燥機に使われている防振ゴム
基礎への伝達力
冒頭で「防振ゴム」を説明した理由は、本議題の「基礎への伝達力」の理解に不可欠だからです。
機械設計において振動は不要なものであり、振動発生源(モーターやエンジンなど)とそれを支える基礎や床、フレームといった構造物に振動が伝わらないようにする必要があります。
この時に、ゴムやタイヤ、バネによる結合・締結・支持が用いられます。
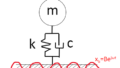
ここで、振動発生源のモーターやエンジンなどを質点と考え、ゴムなどの支持部材をバネとすると、下図のような1自由度粘性減衰系でモデル化することができます。

ちなみに、上図はわたくし(MATLABパイセン)のTwitterのアイコンでもあります。
上図において、振動している質量と基礎を結ぶのは、cのダンパとkのバネです。
この2つを介して、力が基礎に伝達します。
バネによる力は\( kx(t) \)、ダンパによる力は\( c\dot{x(t)} \)です。
ここで、式(2.104)から変位は速度より位相角がπ/2遅れていることがわかります。
$$
\dot{x(t)} = jωXe^{jωt} =ωXe^{j(ωt+π/2)} \tag{2.104}
$$
Xを用いて書き換えると、バネによる力はk|X|、ダンパによる力はcω|X|になります。
この両者の力は位相角π/2が生じているので、2つの合力の大きさは式(2.105)になります。
$$
F_t =|X| \sqrt{k^2+c^2ω^2} \tag{2.105}
$$
このFtと加振力の振幅Fの比λは式(2.106)となります。
「mに作用する力は考えないのか?」と疑問に思う方もいるかもしれませんね。
疑問に思っている方はFBD(Free Body Diagram)や作用反作用の考え方で、この1自由度の振動系を考えてみてください。
mに作用した力によって、バネやダンパに力が発生します。バネやダンパによる力によって、基礎が反力を返します。つまり、基礎に力が伝搬します。
つまり、バネやダンパの力はmに作用する力を考慮していることになります。
$$
λ = \frac{F_t}{F} = \frac{|X|}{kX_{st}}\sqrt{k^2+c^2 ω^2} = \frac{|X|}{X_{st}}\sqrt{1+( \frac{cω}{k})^2} \tag{2.106}
$$
前回紹介した式(2.92)とcω/k = 2ζβを代入すると式(2.107)が得られる。
$$
\frac{X}{X_{st}} = \frac{1}{ 1 – β^2 + 2jζβ } \tag{2.92}
$$
$$
λ = sqrt{\frac{1+(2ζβ)^2}{ 1 – β^2 + 2jζβ }} \tag{2.107}
$$
λを振動伝達率と呼びます。
では、簡単にζを変化させた時のλを図示してみましょう。結果は下図になります。
上記の結果からわかることは下記です。
・β=√2のときに、ζに無関係にλが1になる。
・基礎や床への振動の伝達を避けるためには、βを大きくしたほうがいい。
つまり、運転周波数ωを高くしたほうが良い
or
ゴムのばね定数kを低くしてΩを低くする
clear all;clc;close all;
k=1000; %ばね定数
m=1; %質量
% % c=1; %減衰c
% % cc=2*sqrt(m*k); %臨界減衰係数
Omega=sqrt(k/m); %固有値
freq=0.001:0.001:20; %周波数
w=2*pi*freq; %角周波数
beta=w/Omega;
% zeta=c/cc;
zeta=0:0.1:1;
j=sqrt(-1);
RGB=jet(length(zeta));
figure
for ii1=1:length(RGB)
Lamda=sqrt( (1+(2*zeta(ii1).*beta).^2) ./ ((1-beta.^2).^2+(2*zeta(ii1).*beta).^2) );
plot(beta,Lamda,'color',RGB(ii1,:))
hold on
grid on
end
plot([0 sqrt(2)],[1 1],'k--','linewidth',3)
plot([sqrt(2) sqrt(2)],[0 1],'k--','linewidth',3)
legend(split(num2str(zeta)))
text(1.5,1,'(√2 , 1)')
ylim([0 3])
xlim([0 3])
xlabel('β=ω/Ω')
ylabel('λ')
今日の解説はここまで。
Good luck

コメント