はじめに
過去にモード同定法(カーブフィット)について理論やMATLABプログラムを解説しました。例えば、半値幅法やモード円適合、プロニー法(ポリレファレンス法)、偏分反復法、RFP法にバネマスモデルで同定精度などを検証していました。
上記記事は理論を理解するのに有効だったかと思います。読者の一部には「ネットのよくわからん輩が作ったコードではなく、MATLABのライブラリ関数を利用したい」という方もいるかと思います。
そんな方にオススメなのが”Signal Processing Toolbox”の関数である”modalfit“です。”modalfit“の詳細はリンクのMathWorksのドキュメンテーションをご確認ください。ちなみに、”modalfit”には’lsce’と’lsrf’,’pp’という3手法が使えます。
ただ、カーブフィットマニアの間では「”modalfit”の精度が良くない」と噂されていました。私自身は”modalfit”を使ったことがなかったので、この度精度検証をしてみました。
私自身もカーブフィットソフトを作成しました。ご興味のある方は下記でダウンロードできますので、お試しください。
👉無料ダウンロード
👉マニュアルページ
検証内容
下図のような4自由度のバネマスモデルを考えます。とりあえず、適用にkとmを決めてモードベクトルを求め、設定した共振周波数とモード減衰をmodalfitで推定できるのかを検証します。「とりあえず、適当」で良い理由は、今回はカーブフィットの精度を検証したいので、後から「真値の共振周波数」を設定した方が都合がいいです。
モード法でFRFや応答を計算する場合、モード質量、モード剛性、モードベクトルが必要になります。モードベクトルは共振周波数によらず形状(値)が同じです。また、モード質量は1、モード剛性は固有値(角共振周波数の二乗)です。つまり、数値計算上の検証ではモードベクトルだけとりあえず先に計算しておいて、後から共振周波数を設定してもモード剛性とモード質量を構成することができます。
今回は共振周波数を1~4次の共振周波数をキリの良い数値に指定しておいた方が”modalfit”の精度をぱっと見で検証するには便利です。
ここで、真値の共振周波数は10, 100, 1000, 1500Hzとしましょう。

MATLABコードはこんな感じです。
N = 4; % 共振周波数の数
m_vec=ones(1,N);
k_vec=ones(1,N)*10^7;
[M]=eval_Mmatrix(m_vec); %質量行列
[K]=eval_Kmatrix(k_vec); %剛性行列
[V,D]=eig(K,M); %固有値D、固有ベクトルV
fn=[10 100 1000 1500]; %後から共振周波数を設定する
wn=2*pi*fn;
kr=wn.^2; % モード剛性
mr=ones(1,N);% モード質量
function [K]=eval_Kmatrix(k_vec)
K=zeros(length(k_vec));
for ii1=1:length(k_vec)
if ii1==1
K(ii1,ii1)=k_vec(ii1);
else
K(ii1-1:ii1,ii1-1:ii1)=K(ii1-1:ii1,ii1-1:ii1)+[1 -1;-1 1]*k_vec(ii1);
end
end
end
function [M]=eval_Mmatrix(m_vec)
M=diag(m_vec);
end
まずはモード減衰比を0.5%で設定して、共振周波数とモード減衰比にランダムノイズ(0.5%以下)を加えたときのFRFを1つ(1加振1応答)の結果を用いて推定精度がどうなるのかを検証してみます。
次にモード減衰比を変えて、精度がどのように推移するのか検証します。なお、モード減衰比の大きさに比例して、共振周波数とモード減衰比に加えるノイズも大きくしました。
検証結果(モード減衰比 約0.5%の場合)
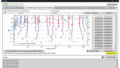
さっそく結果を下図に示します。下図は横軸にモード次数を、縦軸に真値と”modalfit”で推定した値との誤差を示しています。参考までに過去に紹介したRFP法も比較しています。図に示すように、”modalfit”の手法’lsce’では誤差が大きいことがわかります。また3次以上ではNaNとなってしまいグラフ化できませんでした。手法’lsce’の誤差が大きすぎて、他の手法との差がわからないですね。

手法’lsce’を除いた結果が下図です。図に示すように、手法’lsrf’ではそれなりの精度ですね。手法’lsrf’では共振周波数の推定誤差が最大で0.0003%、モード減衰比の推定誤差が0.2%、手法’pp’は共振周波数の推定誤差が最大0.06%、モード減衰比の推定誤差が5.7%です。どちらも実用上は十分な精度になっているかと思います。ちなみに、過去に紹介したRFP法は最も誤差が小さくなりました。
ただし、手法’pp’の説明に下記記載があったので、frfの数を増やせばより精度が改善する可能性があります。frfを増やした場合の検証もやりたいところではありますが、検証工数が多くなりますので、今回は割愛します。
frfごとに 1 つのfnの推定および 1 つのdrの推定をもちます。

検証結果(モード減衰比 約0.5~10%)
各手法で共振周波数を推定した結果が下図です。色がモード減衰比の違いを表しています。図からわかるように,”modalfit”の手法’lsce’では誤差が大きいことがわかります。また、手法’lsrf’および’pp’ではモード減衰比が大きくなるにつれて共振周波数の推定誤差が増加しています。モード減衰比が10%のときの手法’lsrf’での共振周波数の推定誤差は0.8%程度です。実用上は問題ないレベルの誤差かと思われます。繰り返しになりますが、過去に紹介したRFP法は最も誤差が小さくなりました。

次にモード減衰比の推定精度を下図に示します。図からわかるように,”modalfit”の手法’lsce’および’pp’ではモード減衰比の精度が非常に悪いことがわかります。手法’lsrf’ではモード減衰比の推定誤差が最大で9.5%程度です。仮に、真値のモード減衰比が10%でモード減衰の推定誤差が10%の場合、推定したモード減衰は9%もしくは11%になります。この程度の差であれば実用上は問題ないと考えられ、手法’lsrf’であれば使用しても問題ないと考えられます。またまた繰り返しになりますが、過去に紹介したRFP法は最も誤差が小さくなりました。

ということで、”modalfit”を用いてモード同定する場合は手法’lsrf’を使うのが無難であると考えられます。
実行コード
clear all;clc;close all
N = 4; % 共振周波数の数
freq=1:1:2000; %計算周波数の定義
df=freq(2) - freq(1);
w=2*pi*freq; %角振動数
m_vec=ones(1,N);
k_vec=ones(1,N)*10^7;
[M]=eval_Mmatrix(m_vec); %質量行列
[K]=eval_Kmatrix(k_vec); %剛性行列
[V,D]=eig(K,M); %固有値D、固有ベクトルV
for ii1=1:length(m_vec)
V(:,ii1)=V(:,ii1)/V(1,ii1); % 加振点m1のモードベクトルの成分が1になるように正規化
end
% % % % % % モードベクトルVは↑の結果を使って、検証しやすいようにモード質量とモード剛性は再設定
noise_coef=[0.005 0.01:0.01:0.1];
% noise_coef=[0.005 ];
mr=ones(1,N);
F=zeros(length(m_vec),1); F(1)=1; %外力ベクトル(全周波数帯を1で加振する)
N2=100;
modalfit_check.lsce.fn=zeros(N2,length(noise_coef),N);
modalfit_check.lsce.md=zeros(N2,length(noise_coef),N);
modalfit_check.lsrf.fn=zeros(N2,length(noise_coef),N);
modalfit_check.lsrf.md=zeros(N2,length(noise_coef),N);
modalfit_check.pp.fn=zeros(N2,length(noise_coef),N);
modalfit_check.pp.md=zeros(N2,length(noise_coef),N);
RFPM.fn=zeros(N2,length(noise_coef),N);
RFPM.md=zeros(N2,length(noise_coef),N);
for iin=1:length(noise_coef)
for iin2=1:N2
noise = rand(1,N)*noise_coef(iin) + ones(1,N) ;
fn=[10 100 1000 1500].*noise;
wn=2*pi*fn;
kr=wn.^2;
c_cr=2*sqrt(mr.*kr);
modal_dampimg=noise_coef(iin)*noise(1); %モード減衰比(とりあえず4%と設定)
cr=c_cr.*modal_dampimg; %モード減衰係数
Xj=zeros(1,length(freq)); %変位ベクトル(計算前にベクトルを定義してメモリを確保)
% % % % モード法
ii=1; %加振点 (加振点が複数ある場合はfor ii=1:kength(F)のループを追加すればよい )
for ii1=1 %応答点
for ii2=1:length(wn)
Xj(ii1,:)=Xj(ii1,:)+V(ii1,ii2)*V(ii,ii2)./( -mr(ii2).*w.^2 + 1i*cr(ii2)*w +kr(ii2) )*F(ii);
% 横ベクトル =横ベクトル + スカラー ×スカラー ./( スカラー×横ベクトル + スカラー×横ベクトル +スカラー)×スカラー
end
end
FRF_E=Xj(1,:);
ideal_md=modal_dampimg; ideal_fn=fn;
[fn2,dr2] = modalfit(FRF_E.',freq.',freq(end)*2,4,'FitMethod','lsce');
modalfit_check.lsce.md(iin2,iin,:)=abs(ideal_md - dr2)/ideal_md;
modalfit_check.lsce.fn(iin2,iin,:)=abs(ideal_fn - fn2.')./ideal_fn;
[fn2,dr2] = modalfit(FRF_E.',freq.',freq(end)*2,4,'FitMethod','lsrf');
modalfit_check.lsrf.md(iin2,iin,:)=abs(ideal_md - dr2)/ideal_md;
modalfit_check.lsrf.fn(iin2,iin,:)=abs(ideal_fn - fn2.')./ideal_fn;
[fn2,dr2] = modalfit(FRF_E.',freq.',freq(end)*2,4,'FitMethod','pp');
modalfit_check.pp.md(iin2,iin,:)=abs(ideal_md - dr2)/ideal_md;
modalfit_check.pp.fn(iin2,iin,:)=abs(ideal_fn - fn2.')./ideal_fn;
[FRF_recalcu,modal_parameter]=Rational_Fraction_Polynomial_Method(FRF_E,freq,4);
RFPM.md(iin2,iin,:)=abs(ideal_md - modal_parameter(:,2))/ideal_md;
RFPM.fn(iin2,iin,:)=abs(ideal_fn - modal_parameter(:,1).'/(2*pi))./ideal_fn;
end
end
% % save('all_20240501.mat')
function [K]=eval_Kmatrix(k_vec)
K=zeros(length(k_vec));
for ii1=1:length(k_vec)
if ii1==1
K(ii1,ii1)=k_vec(ii1);
else
K(ii1-1:ii1,ii1-1:ii1)=K(ii1-1:ii1,ii1-1:ii1)+[1 -1;-1 1]*k_vec(ii1);
end
end
end
function [M]=eval_Mmatrix(m_vec)
M=diag(m_vec);
end
function [FRF_recalcu,modal_parameter]=Rational_Fraction_Polynomial_Method(FRFdata,freq,N)
% modal_parameter = Modal Parameters [freq,damp,Ci,Oi]:
% fn:共振周波数
% damp:モード減衰比
% Ci:モード振幅
% Oi:モード位相角
% % % % % % % % % % % % % % % % % 初期設定
w=2*pi*freq;
[r,c]=size(w);
if r<c
w=w.';
end
[r,c]=size(FRFdata);
if r<c
FRFdata=FRFdata.';
end
% % 角周波数の正規化
nom_w=max(w);
w=w./nom_w;
% % % % % % % % % % % % % % % % % % % % % % % % % %
m=2*N-1; %式(4.60OT)のm
n=2*N; %式(4.60OT)のn
%orthogonal function that calculates the orthogonal polynomials
[phi,coeff_A]=Complex_Orthogonal_Polynomials(FRFdata,w,1,m);
[theta,coeff_B]=Complex_Orthogonal_Polynomials(FRFdata,w,2,n);
[r,c]=size(phi);
P=phi(:,1:c); %式(4.66OT)のP
[r,c]=size(theta);
Theta=theta(:,1:c); %式(4.67OT)のθ
T=sparse(diag(FRFdata))*theta(:,1:c-1);
W=FRFdata.*theta(:,c);%式(4.66OT)のW
X=-2*real(P'*T); %式(4.70OT)の最左の行列(1,2)
G=2*real(P'*W); %式(4.70OT)の最右のベクトル(1,1)
D=-inv(eye(size(X))-X.'*X)*X.'*G; %式(4.72OT)
C=G-X*D; %式(4.73OT)
D=[D;1];
%calculation of FRF (alpha)
FRF_recalcu=zeros(length(w),1);
for n=1:length(w),
numer=sum(C.'.*P(n,:));
denom=sum(D.'.*Theta(n,:));
FRF_recalcu(n)=numer/denom;
end
A=coeff_A*C;
[r,c]=size(A);
A=A(r:-1:1).'; %{A} standard numerator polynomial coefficients
B=coeff_B*D;
[r,c]=size(B);
B=B(r:-1:1).'; %{B} standard denominator polynomial coefficients
%calculation of the poles and residues
[R,P,K]=residue(A,B);
[r,c]=size(R);
for n=1:(r/2),
Residuos(n,1)=R(2*n-1);
Polos(n,1)=P(2*n-1);
end
[r,c]=size(Residuos);
Residuos=Residuos(r:-1:1)*nom_w; %residues
Polos=Polos(r:-1:1)*nom_w; %poles
fn=abs(Polos); %Natural frequencies (rad/sec)
damp=-real(Polos)./abs(Polos); %Damping ratios
Ai=-2*(real(Residuos).*real(Polos)+imag(Residuos).*imag(Polos));
Bi=2*real(Residuos);
const_modal=complex(Ai,abs(Polos).*Bi);
Ci=abs(const_modal); %Magnitude modal constant
Oi=angle(const_modal).*(180/pi); %Phase modal constant (degrees)
modal_parameter=[fn, damp, Ci, Oi]; %Modal Parameters
end
% % % % % % % % % % % % % % % % % % % % %
function [P,coeff]=Complex_Orthogonal_Polynomials(FRFdata,w,phitheta,kmax)
if phitheta==1
q=ones(size(w)); %分子項(bの項)の重み関数
elseif phitheta==2
q=(abs(FRFdata)).^2; %分母項(aの項)の重み関数
end
R_m1=zeros(size(w)); %式(4.1004)
R_0=1/sqrt(2*sum(q)).*ones(size(w)); %式(4.1005)
Rminus=[R_m1,R_0]; %polynomials Half Function
coeff=zeros(kmax+1,kmax+2);
coeff(1,2)=1/sqrt(2*sum(q));
%generating orthogonal polynomials matrix and transform matrix
Rplus=[];
R=[Rminus Rplus];
for k=1:kmax,
Vkm1=2*sum(w.*R(:,k+1).*R(:,k).*q); %IMACの論文の(29)式
Sk=w.*R(:,k+1)-Vkm1*R(:,k); %式(4.1006)
Dk=sqrt(2*sum((Sk.^2).*q)); %IMACの論文の(31)式
Rplus=[Rplus Sk/Dk];
coeff(:,k+2)=-Vkm1*coeff(:,k);
coeff(2:k+1,k+2)=coeff(2:k+1,k+2)+coeff(1:k,k+1);
coeff(:,k+2)=coeff(:,k+2)/Dk;
R=[Rminus Rplus];
end
R=R(:,2:kmax+2); %orthogonal polynomials matrix
coeff=coeff(:,2:kmax+2); %transform matrix
P=R.*i.^(0:kmax); %式(4.1003)
jk=i.^(0:kmax);
coeff=(jk'*jk).*coeff;
end

コメント