MATLABで学ぶ音響工学　閉空間（直方体）3

前回の記事では閉空間内の音圧の算出方法について説明しました。もっと詳細内容が知りたい方は下記の参考文献をご確認ください。

MATLABで学ぶ音響工学　閉空間（直方体）2

今回は閉空間内の音圧の算出方法について紹介します。 なお、式の導出過程が難しいので、最終的な式のみを記載します。 （詳しい導出過程は右記参考文献でお願いします→P.A. Nelson, "Active Control of Sound", Academic Press(1993)）

mech-eng-uni.com

2021.03.18

ただし、前回はFRFのみを算出したため、その結果を考察することが難しかったです。今回はその結果を可視化したいと思います。

1次の共振周波数の結果

2次の共振周波数の結果

5次の共振周波数の結果

入力点が(0,0,0)なのと、1次の音響モードがうまく表現できているので、おそらく計算は正しいと思われます。

次回は、音場を制御方法について説明したいと思います。

下記プログラム内で使っているfunctionファイルのThreeDploter_linについては、また日を改めて説明いたします。
今回はこのへんでGood luck

メインコード（実行コード）

clear all
% addpath('E:\function')
% % % % size of rectangular parallelopiped 
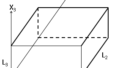
L1=1.9;
L2=1.3;
L3=1.2;
V=L1*L2*L3;
% % % % Constant value
co=344;
rho=1.205;
Zeta=0.001;
% % % % modal numbers
n_max=20;
Combi=combinator(n_max,3,'p','r')-1;
% % % % setting max frequency
f_max=2000;
freq=0:2:f_max;
w=2*pi*freq.';
% % % % xi=(x1,x2,x3)
xi=get_geo(L1,L2,L3,7,7,7);
% % % % y_secondary_i=(ys1,ys2,ys3)
ysi=[0 0 0];
% % % % function wn
[wn]=angular_frequency(Combi,L1,L2,L3,co);
% % % % function psi psi(modal number , x_number)
[psix_front]=Psi(xi,Combi,L1,L2,L3);
[psiy]=Psi(ysi,Combi,L1,L2,L3);
% % % % sort of wn in order to get n
[wn,I] =sortrows(wn);
% % % % % % % % Select appropriate modes
% for n=1:length(wn)
%     if wn(n)<=f_max*2*pi*1.5
%     Wn(n,1)=wn(n);
%     else
%         break
%     end
% end
Wn(1:4420,1)=wn(1:4420,1);
Psiy=psiy(I(1:length(Wn)),:);
PsiX=psix_front(I(1:length(Wn)),:);
% % % % % % % % % % % % % % % 
G0=cellzeros(size(xi,1),size(ysi,1),length(freq));
% % % % % % % % % % % % % % % %
h = waitbar(0,'Please wait...');
for nx=1:1:size(xi,1)
    for ny=1:1:size(ysi,1)
            for n=1:length(Wn)
                G0{nx,ny}(1:length(freq))=w.*rho*co^2......
                    ./ ( V *( 2*Zeta*Wn(n).*w + i*(w.^2 - Wn(n)^2) ) ).....
                    *Psiy(n,ny)*PsiX(n,nx).....
                    +G0{nx,ny}(1:length(freq));                                
            end
    end
       waitbar(nx/size(xi,1),h)
end
close(h)
id=91;
g=cell2matrix(G0,id);
figure
ThreeDploter_lin(20*log10(g),100,xi,2,'o')
title(num2str(freq(id)))
axis equal
grid on
% save('G0.mat','G0')
% save all.mat

function geo=get_geo(L1,L2,L3,nl1,nl2,nl3)

x1=linspace(0,L1,nl1);
x2=linspace(0,L2,nl2);
x3=linspace(0,L3,nl3);

geo=zeros(nl1*nl2*nl3,3);
n=0;
for ii2=1:nl2
    for ii3=1:nl3
        n=n+1;
            geo(1+nl1*(n-1):nl1*n,:)=[x1.' ones(nl2,1)*x2(ii2) ones(nl3,1)*x3(ii3)];
    end
end

end

function g=cell2matrix(G,n)

g=zeros(size(G));

for ii1=1:size(G,1)
    for ii2=1:size(G,2)
        g(ii1,ii2)=G{ii1,ii2}(n);
    end
end