前回の記事では閉空間の固有値と固有ベクトル(共振周波数とモードベクトル)の算出方法のプログラムを紹介いたしました。

今回は閉空間内の音圧の算出方法について紹介します。
なお、式の導出過程が難しいので、最終的な式のみを記載します。詳しい導出過程は下記参考文献でご確認お願いします。
記事の書き方にもだんだん慣れてきました。これからはもう少し見やすさも意識して書きたいと思います!
前回の紹介した式もそのまま記載しておきます。
$$
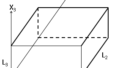
{k_n}^2 = \frac{{ω_n}^2}{{c_o}^2}=[\frac{n_1\pi}{L_1}]^2+[\frac{n_2\pi}{L_2}]^2+[\frac{n_3\pi}{L_3}]^2
$$
kn^2:固有値
wn:固有角振動数
n:モード次数(モード次数というより、「節の数」)
モードベクトル:ψn
$$
{\psi_n(x)}=\sqrt{\epsilon_1 \epsilon_2 \epsilon_3} \ cos{\frac{n_1\pi x_1}{L_1}} \ cos{\frac{n_2\pi x_2}{L_2}} \ cos{\frac{n_3\pi x_3}{L_3}}
$$
ε:正規化係数(詳細は前回の記事へ)
音圧pは下式で表現できる。
$${p(x)}=\sum_{n=1}^{\infty}a_n \psi_n(x)$$
$$ a_n = \frac{ω_n ρ_o {c_o}^2}{V [2 ζ_n ω_n ω + j (ω^2-{ω_o}^2)]} q_p \psi_n(y_p) $$
ここで、q_pは入力音源の入力値で、psi_n(y_p)は入力位置のモードベクトルです。
ここで、入力と応答間のFRF(周波数応答関数)G(ω)は下式になります。
$${G(ω)}=\frac{p(x)}{q_p }$$
下のプログラムを実行すると、下記結果が得られます。本プログラムの応用については次回の記事で説明したいと思います。

メインコード(実行コード)
今回はこのへんでGood luck
clear all
% addpath('E:\function')
% % % % size of rectangular parallelopiped
L1=1.9;
L2=1.3;
L3=1.2;
V=L1*L2*L3;
% % % % Constant value
co=344;
rho=1.205;
Zeta=0.001;
% % % % modal numbers
n_max=100;
Combi=combinator(n_max,3,'p','r')-1;
% % % % setting max frequency
f_max=2000;
freq=0:1:f_max;
w=2*pi*freq.';
% % % % sampling number
d=0.1;
% % % % xi=(x1,x2,x3)
xi=[0 0 0
0.5 0.5 0.5
1 1 1
1.5 1 1];
% % % % y_secondary_i=(ys1,ys2,ys3)
ysi=[0 0 0
1 0 0];
% % % % function wn
[wn]=angular_frequency(Combi,L1,L2,L3,co);
% % % % function psi psi(modal number , x_number)
[psix_front]=Psi(xi,Combi,L1,L2,L3);
[psiy]=Psi(ysi,Combi,L1,L2,L3);
% % % % sort of wn in order to get n
[wn,I] =sortrows(wn);
% % % % % % % % Select appropriate modes
% for n=1:length(wn)
% if wn(n)<=f_max*2*pi*1.5
% Wn(n,1)=wn(n);
% else
% break
% end
% end
Wn(1:4420,1)=wn(1:4420,1);
Psiy=psiy(I(1:length(Wn)),:);
PsiX=psix_front(I(1:length(Wn)),:);
% % % % % % % % % % % % % % %
G0=cellzeros(size(xi,1),size(ysi,1),length(freq));
% % % % % % % % % % % % % % % %
h = waitbar(0,'Please wait...');
for nx=1:1:size(xi,1)
for ny=1:1:size(ysi,1)
for n=1:length(Wn)
G0{nx,ny}(1:length(freq))=w.*rho*co^2......
./ ( V *( 2*Zeta*Wn(n).*w + i*(w.^2 - Wn(n)^2) ) ).....
*Psiy(n,ny)*PsiX(n,nx).....
+G0{nx,ny}(1:length(freq));
end
end
waitbar(nx/size(xi,1),h)
end
close(h)
figure
plot(freq,abs(G0{2,1}),'b')
hold on
plot(freq,abs(G0{3,1}),'r')
plot(freq,abs(G0{4,1}),'g')
% save('G0.mat','G0')
function [A]=cellzeros(n1,n2,lengthnakami)
A=cell(n1,n2);
for n11=1:n1
for n22=1:n2
A{n11,n22}(1:lengthnakami,1)=zeros(lengthnakami,1);
end
end
end
ちなみに前回の記事に記載したfunctionファイルも使用するので、そのファイルは下記にて参照ください。



コメント