はじめに
振動工学やモード解析をご存じの方であれば、一度は読んだことがあると言われているバイブル的な書籍「モード解析入門」について再復習しております。 今回は6.3.2項の「プロニー法」P.367から復習します。プロニー法を多点参照法に拡張したものが「ポリレファレンス法」です。(ボルドーが立案したので「ボルドーの方法」)とも呼ばれます。
MATLAB2017aのSignal Processing Toolboxから導入されたmodalfitという関数でのモード同定手法では「プロニー法」でも解くことができるようです。詳しくはMathWorksさんのサイトを参照ください。ちなみに、modalfitのデフォルトのモード同定手法であるFitMethod=lsceがProny法(プロニー法)と説明されています。
モード解析入門について他の章も解説しているので、過去の記事を読んでいない方、この章や節以外を復習したい方は下記記事を参照ください。
下記記事が目次となっており、各章や節にアクセスできるようにしています。

私自身もカーブフィットソフトを作成しました。ご興味のある方は下記でダウンロードできますので、お試しください。
👉無料ダウンロード
👉マニュアルページ
6.3.2 プロニーの方法
これまでの記事で、FRFや振動形状はモード特性(共振周波数&振動モードなど)の重ね合わせで表現できるということを説明しましたね。この考え方がモード解析である、ということは理解頂けていると思います。そして、FRFからモード特性を抽出することをモード同定と呼びます。
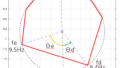
モード円適合(カーブフィット)や半値幅法は、図1の赤色の周波数帯のように隣り合う共振周波数が十分離れており、1自由度系と見なせる場合にのみ適用可能な手法でした。
 図1 FRF
図1 FRF
一方、プロニーの方法は多自由度系のモード同定手法です。つまり、図1の0~100Hzのデータのように複数の共振周波数を含んでいても、それぞれのモード特性を抽出することができる手法です。
ここからは少し専門的な説明になります。
プロニーの方法は、単位衝撃応答のデータからモード特性を推定する手法です。インパクトハンマーなどで打撃加振した応答の時刻歴データを使ってもいいですが、一般的にはSN比が悪くなることが知られており、測定回数分で平均化したFRFを逆fftして、インパルス応答に戻したデータをプロニー法の入力とする場合が多いです。
インパルス応答はモード特性の重ね合わせで表現できるので、式(6.52)のように表現できます。
$$
h(t)=\sum_{r=1}^{N} a_{r}(je^{λ_r t} – je^{λ_r^* t} ) \tag{6.52}
$$
ここで、λrは固有値、ωdrは減衰固有角振動数、σrはモード減衰率で、詳細は下式です。
$$
a_r=\frac{ Ω_r^2 }{2ω_{dr}K_r}, λ_r=-σ_r + jω_{dr}, λ_r^*=-σ_r – jω_{dr} \tag{6.51}
$$
ただし、上式よりも、arは留数、λrは固有値、ωdrは減衰固有角振動数、σrはモード減衰率とだけ覚えておけば良いと思います。
繰り返しになりますが、モード同定は留数arと固有値λrを求めることを意味します。
モード同定には様々な手法がありますが、留数arと固有値λrを求めるためのアプローチ方法が違うだけです。
データは離散化されているので、時刻tも離散化した形で表すと式(6.53)は式(6.54)のようになります。なお、iはデータid(番号)です。また全共振周波数の数Nを全て同定するのではなく、Nの内のn(n<N)だけ同定することを想定します。
$$
h(iΔt)=\sum_{r=1}^{n} a_{r}(e^{λ_r iΔt} – e^{λ_r^* iΔt} ) \tag{6.52}
$$
ここで、文字式が煩雑になるため、簡略化のために下記のように置き換えます。
$$
x_r=e^{λ_r Δt}, x_r^*=e^{λ_r^* Δt} \tag{6.55}
$$
すると、式(6.56)のように表せます。
$$
h(iΔt)=\sum_{r=1}^{n} a_{r}(x_r^i + x_r^{i*} )=\sum_{r=1}^{n} real( 2a_{r}(x_r^i ) )=\sum_{r=1}^{2n} a_{r}(x_r^i ) \tag{6.56}
$$
式(6.56)の式展開が理解できない方がいると思います。もともとはn個の共振周波数を同定することを前提に式展開していましたが、2n個同定することにしたほうが式のまとまりが良いので、2nにしました。なお、2n<Nとします。(まあNは理論展開の話なので、実際のプログラムでは2n>Nでも解けますが…..)
ここまではなんとかついてこれますよね。
式(6.56)は式変形を繰り返しただけで、このままでは留数arと固有値λrを抽出できませんね。
とりあえず、式(6.56)を簡単な形にして考えてみましょう。n=2、i=0,1,2,3,4のときを考えます。
\(
h(0)=a_1 x_1^0 + a_2 x_2^0 + a_3 x_3^0 + a_4 x_4^0
\\
h(1)=a_1 x_1^1 + a_2 x_2^1+ a_3 x_3^1 + a_4 x_4^1
\\
h(2)=a_1 x_1^2 + a_2 x_2^2 + a_3 x_3^2 + a_4 x_4^2
\\
h(3)=a_1 x_1^3 + a_2 x_2^3 + a_3 x_3^3 + a_4 x_4^3
\\
h(4)=a_1 x_1^4 + a_2 x_2^4 + a_3 x_3^4 + a_4 x_4^4
\)
$$
\tag{6.56.0}
$$
この状態では留数arと固有値λrを抽出できませんね。
そこで、下記を考えます。
$$
(x-x_1)(x-x_1^*)(x-x_2)(x-x_2^*) =0 \tag{6.57.3}
$$
手計算するのが大変なので、Maximaで解けるように下記のように置き換えます。
$$
(x-a1)(x-c1)(x-a2)(x-c2) =0
$$
上式を展開すると
\(
x^4 \\ +(-c2-c1-a2-a1)x^3 \\ +(c1*c2+a2*c2+a1*c2+a2*c1+a1*c1+a1*a2)x^2 \\ +(-a2*c1*c2-a1*c1*c2-a1*a2*c2-a1*a2*c1)x \\ +a1*a2*c1*c2 =0
\)
$$
\tag{6.57.0}
$$
上記を下記のように置き換えます。なお、ここではb4=1です。
\(
b_4 x^4 \\ +b_3 x^3 \\ +b_2 x^2 \\ +b_1 x^1 \\ +b_0 x^0 =0
\)
$$
\tag{6.57.1}
$$
式(6.57.1)式を一般化したものが式(6.57)です。
$$
\sum_{i=0}^{2n}b_i x^i =0 \tag{6.57}
$$
では、ここで式(6.56.0)と式(6.57.1)を見比べつつ、留数arと固有値λrを抽出方法を考えます。とりあえず、式(6.56.0)の両辺にbiをかけてみます。
\(
b_0 h(0)=b_0 (a_1 x_1^0 + a_2 x_2^0 + a_3 x_3^0 + a_4 x_4^0)
\\
b_1 h(1)=b_1 (a_1 x_1^1 + a_2 x_2^1+ a_3 x_3^1 + a_4 x_4^1)
\\
b_2 h(2)=b_2 (a_1 x_1^2 + a_2 x_2^2 + a_3 x_3^2 + a_4 x_4^2)
\\
b_3 h(3)=b_3 (a_1 x_1^3 + a_2 x_2^3 + a_3 x_3^3 + a_4 x_4^3)
\\
b_4 h(4)=b_4 (a_1 x_1^4 + a_2 x_2^4 + a_3 x_3^4 + a_4 x_4^4)
\)
$$
\tag{6.60.0}
$$
式(6.60.0)を全て足し合わせてまとめると下記になります。
$$
\sum_{i=0}^{2*2}b_i h(i) = a_1 \sum_{i=0}^{2*2}b_i x_1^i +a_2 \sum_{i=0}^{2*2}b_i x_1^i +a_3 \sum_{i=0}^{2*2}b_i x_3^i +a_4 \sum_{i=0}^{2*2}b_i x_4^i \tag{6.60.1}
$$
式(6.57)より、式(6.60)は式(6.61.0)となります。
$$
\sum_{i=0}^{2*2}b_i h(i) = 0 \tag{6.61.0}
$$
式(6.61.0)を少し変形します。
$$
b_4 h(4) + \sum_{i=0}^{2*2-1}b_i h(i) = 0 \tag{6.61.1}
$$
ここで、b4=1なので下式が成立します。
$$
-h(4) = \sum_{i=0}^{2*2-1}b_i h(i) \tag{6.62.0}
$$
モード解析入門では上記を一般化した説明があります。ただし、私のようなゴリゴリのモード同定マニアであれば、もう少し違った説明をしたいので補足を加えたいと思います。
例えば、図2のようなインパルス応答でi=0~2n-1 の時刻歴データは0.1秒分であったとします。
時間分解能を0.0001とすると、インパルス応答の0.1秒分の取り方は、
0~0.1秒でも良いし、
0.0001~1.0001秒でもいいですよね。
 図2 インパルス応答
図2 インパルス応答
そこで、たくさんの0.1秒分のデータを使って誤差が最小となるようなbを算出するという方法が知られています。具体的には式(6.62.1)~式(6.62.3)のように解きます。
\(
\left(
\begin{array}{ccc}
h(0) & \ldots & h(2n-1) \\
\vdots & \ddots & \vdots \\
h(2n-1) & \ldots & h(4n-2)
\end{array}
\right)
\left(
\begin{array}{c}
b_0 \\
\vdots \\
b_{2n-1}
\end{array}
\right)=
\left(
\begin{array}{c}
h(2n) \\
\vdots \\
h(4n-1)
\end{array}
\right) \tag{6.62.1}
\)
上式を簡略化したものが、式(6.62.2)です。
$$
Hb=y \tag{6.62.2}
$$
yに誤差が含まれてると考えて、最小二乗法でbを解いたものが式(6.62.3)です。
$$
b=(H^tH)^{-1} H^t y \tag{6.62.2}
$$
これでbが求まりましたね。
bが求まると、式(6.57)の代数方程式を解くと式(6.55)のxrが求まります。
xrから、下式のように減衰角共振周波数ωdr、モード減衰率σrを求めます。
$$
σ_r=-\frac{In|x_r|}{Δt} \tag{6.100.1}
$$
$$
ω_{dr}=\frac{1}{Δt}atan(\frac{imag(x_r)}{real(x_r)}) \tag{6.100.2}
$$
上記までの理論式がモード解析ハンドブックなどのモード同定に記載されているかと思います。
ただし、上記理論式だけではモード特性を同定できません。というより、プロニー法では共振周波数の数を多めに同定することなります。例えば、2つしか共振周波数が励起されていない波形を、プロニー法では50つの共振周波数があると仮定してモード特性を推定します。
そのため、推定した50つの中から正しいそうな2つを抽出する必要があります。そもそも50つの中で正しく推定できていない場合もあります。これらを判断する必要がありますが、その判断指標については、市販の参考書には記載されていません。
上記の課題については例題を用いて説明したいと思います。
MATLABで示す例題
式(6.62.2)までの解法
ここからは、例題をMATLABで解いていきましょう。
図3のような共振周波数が10Hzおよび50Hzのインパルス応答波形から、モード特性を求めてみましょう。なお、モード減衰比は5%@10Hz、1%@50Hzです。
 図3 インパルス応答波形
図3 インパルス応答波形
では、図4の波形を作ってみましょう。MATLABのプログラムは下記のようになります。
clear all;clc;close all;
j=sqrt(-1);
time=0:0.0001:1;
% % 時刻歴応答ベクトルXの例
freq1=10; omega1=freq1*2*pi;
freq2=50; omega2=freq2*2*pi;
zeta1=0.05; sgm1=zeta1*omega1;
zeta2=0.01; sgm2=zeta2*omega2;
phi1=0; phi2=0;
X=exp(-zeta1*omega1*time).*sin(omega1*time+phi1)......
+exp(-zeta2*omega2*time).*sin(omega2*time+phi2);
figure
plot(time,X)
xlabel('時間 [s]')
ylabel('振幅 [mm]') %振幅の単位はなんでも良いですが、とりあえずイメージしやすいようにmmにしました
インパルス応答波形が作成できたので、プロニー法の式(6.62.2)までプログラムを作ってみましょう。ちなみにプログラムは下記のようになります。
% 求める共振周波数の数N(とりあえず大きめに設定するのがコツ)
% 求まるのはN-1個
N=10; n=N/2;
% % 式(6.62.1)のH行列の作成
H=zeros(2*n);
for ii1=1:2*n
H(ii1,:)=X(ii1:(ii1+2*n-1)).';
end
% % 式(6.62.1)の右辺(式(6.62.2)yベクトル)
y=-X(2*n+1:n*4).';
% % 式(6.62.2)の最小二乗法
b=(H.'*H)\(H'*y);
式(6.62.2)のbが求まりましたね。
bから式(6.57)を満たすxを求めることでモード特性を求めることができます。
roots関数を用いたモード特性の推定(うまくいかない)
さて、ここからが難しいんですよね。どうやって、式(6.57)を解きますか?
MATLABには多項式の根を求める関数として「roots」があります。
こちらで試してみましょう(先に述べますが、この方法はうまくいきません)
r = roots(b.'); %rootsという関数で式(6.57.3)を解けるらしいが...... % figure % plot(real(r),imag(r),'.') % axis equal % grid on omega_prony = angle(r)/time(2); %式(6.100.2) fn_prony = omega_prony/(2*pi); sgm_prony = -log(abs(r))/time(2); %式(6.100.1) zeta_prony = sgm_prony./omega_prony;
上記プログラムで求まる共振周波数とモード減衰比は下記です。
 図4 求めたモード特性(共振周波数とモード減衰比)
図4 求めたモード特性(共振周波数とモード減衰比)
理論値はfn=10, 50; zeta=0.05, 0.01です。
プロニー法では同定したい次数を大きめに設定する必要があるので、この例題では9つの共振周波数とモード減衰比を推定していますが、理論値と一致する組み合わせはありませんね。
推定する共振周波数の数を増やせば、理論値と一致するような組み合わせが出てくるかもしれません。(おそらく出てくる可能性が高いです。)しかし、膨大な数の共振周波数とモード減衰比の組み合わせから、最もらしい組み合わせを選ぶのは困難です。そもそも、インパルス応答波形に何個の共振周波数が含まれているのかの事前情報なしに推定しているので、組み合わせを選ぶ判断基準が欲しいですね。
ここがモード同定の難しいところです。(モード同定マニアがハマるところです。)
モード同定の理論はたいてい論文や参考書どうりの理論式をプログラム化してもうまくいきません。プログラムを作るためには、理論式の裏に隠れされている情報を紐解いていく必要があります。
提案手法
繰り返しになりますが、bが求まると式(6.57)の等式を満たすxiを求めれば、モード特性を抽出することができると考えられます。
$$
\sum_{i=0}^{2n}b_i x^i =0 \tag{6.57}
$$
では、xiとはどんな値になりそうですか?
そもそも、xiは下記でしたよね。(xrとxiは共振の次数の違いです。r次かi次かの違いです。)
$$
x_r=e^{λ_r Δt} \tag{6.55}
$$
また、λrは下記です。
$$
λ_r=-σ_r + jω_{dr} \tag{6.51}
$$
つまり
$$
x_r=e^{(-σ_r + jω_{dr})Δt}=e^{(-ω_{dr}ζ + jω_{dr})Δt}
$$
モード減衰比ζが現実的に取りうる範囲はどれくらいでしょうか?
経験的に下記ぐらいではないでしょうか?
0<ζ<0.1
次に考えないといけないのは、求めたい共振周波数の範囲です。
今回は例題なのでインパルス応答波形の共振周波数の答えを知っています。
しかし、(事前にスペクトルを確認して、共振周波数のあたり付けをしている場合を除いて)、通常であれば、共振周波数がわかっていてモード同定するということはありません。
モード同定するときは、求めたい周波数範囲を指定して、プロニー法で求める周波数範囲を限定しておくことがポイントです。
例えば、今回の例題では100Hz以下の共振周波数を求めたいとしましょう。(前提として、インパルス応答波形の共振周波数の数や共振周波数自体を知らないで解いていると思ってください)
つまり、共振周波数が存在しそうな範囲は下記です。
0<fn<100
0<ωn<2*pi*100
従って、ζとωnの範囲からx_rも取りうる範囲が決まっています。
MATLABでは下記のようにx(探索用のx_rをxとして定義しています)を定義します。
ここで、xは行方向にζの変化、列方向にωnの変化に対応するようにしています。
そして、式(6.57)の左辺を求めます。
fn_min=0;
fn_max=100;
zeta_min=0.00001; %モード減衰比が0になることはないので、限りなく小さくしておく
zeta_max=0.1;
dt=time(2);
fn_range=fn_min:0.5:fn_max;
wn_range=2*pi*fn_range;
zeta_range=linspace(zeta_min,zeta_max,1000);
x=exp((-zeta_range.'+j)*wn_range*dt);
Eq_6_57=1*x.^(2*n); %b_2n*x.^(2*n)
for ii1=1:2*n
Eq_6_57=Eq_6_57+b(ii1)*x.^(ii1-1); %式(6.57)
end
式(6.57)の左辺であるEq_6_57が0になる、つまり極小値になるようなxを求めることができれば、理論値と一致するようなモード特性が抽出することができると考えられます。
極小値は下記のように求められると考えられます。
% 極の判定・探索 surf_Eq_6_57 = abs(Eq_6_57); surf_pole_logical = islocalmin(surf_Eq_6_57,1) & islocalmin(surf_Eq_6_57,2); % 平面上(行列上)の極小点を探す xr = x(surf_pole_logical); %極 omega_prony = angle(xr)/dt; %式(6.100.2) fn_prony=omega_ans/(2*pi); sgm_prony = -log(abs(xr))/dt; %式(6.100.1) zeta_prony = sgm_prony./omega_prony;
結果は下記のようになりました。しっかり理論値が求められていますね。
 図5 提案手法の結果
図5 提案手法の結果
MATLABプログラム(フルバージョン)
振幅A1とA2を変えても共振周波数とモード減衰比の推定結果が正しくなることなどを確認してみてください
clear all;clc;close all;
j=sqrt(-1);
time=0:0.0001:1;
dt=time(2);
% 求める共振周波数の数N(とりあえず大きめに設定するのがコツ)
% 求まるのはN-1個
N=100; n=N/2;
% % 時刻歴応答ベクトルXの例
A1=1; freq1=10; omega1=freq1*2*pi;
A2=2; freq2=50; omega2=freq2*2*pi;
zeta1=0.05; sgm1=zeta1*omega1;
zeta2=0.01; sgm2=zeta2*omega2;
phi1=0; phi2=0;
X=A1*exp(-zeta1*omega1*time).*sin(omega1*time+phi1)......
+A2*exp(-zeta2*omega2*time).*sin(omega2*time+phi2);
figure
plot(time,X)
xlabel('時間 [s]')
ylabel('振幅 [mm]') %振幅の単位はなんでも良いですが、とりあえずイメージしやすいようにmmにしました
% % 式(6.62.1)のH行列の作成
H=zeros(2*n);
for ii1=1:2*n
H(ii1,:)=X(ii1:(ii1+2*n-1)).';
end
% % 式(6.62.1)の右辺(式(6.62.2)yベクトル)
y=-X(2*n+1:n*4).';
% % 式(6.62.2)の最小二乗法
b=(H.'*H)\(H'*y);
fn_min=0;
fn_max=100;
zeta_min=0.00001; %モード減衰比が0になることはないので、限りなく小さくしておく
zeta_max=0.1;
fn_range=fn_min:0.5:fn_max;
wn_range=2*pi*fn_range;
zeta_range=linspace(zeta_min,zeta_max,1000);
x=exp((-zeta_range.'+j)*wn_range*dt);
Eq_6_57=1*x.^(2*n); %b_2n*x.^(2*n)
for ii1=1:2*n
Eq_6_57=Eq_6_57+b(ii1)*x.^(ii1-1); %式(6.57)
end
% 極の判定・探索
surf_Eq_6_57 = abs(Eq_6_57);
surf_pole_logical = islocalmin(surf_Eq_6_57,1) & islocalmin(surf_Eq_6_57,2); % 平面上(行列上)の極小点を探す
xr = x(surf_pole_logical); %極
omega_prony = angle(xr)/dt; %式(6.100.2)
fn_prony=omega_prony/(2*pi)
sgm_prony = -log(abs(xr))/dt; %式(6.100.1)
zeta_prony = sgm_prony./omega_prony


コメント