MATLABで学ぶ振動工学　N自由度モデル（モード解析）1

スポンサーリンク

はじめに

過去の記事で1自由度モデルの振動理論について簡単に説明しました。
正直なところ、1自由度モデルはプログラムがわからなくても教科書を読めばわかります。
ただし、多自由度モデル（N自由度モデル）ではプログラムがわからないと完全には理解できません。
教科書では多自由度モデルの説明で、3自由度モデルを扱うことがあります。
3自由度モデルだと自力で運動方程式を立てれば、共振周波数などが計算できるため、今後説明する予定の「モード解析」をするメリットを理解することが難しいです。

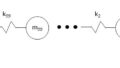
そこで、本記事ではN＝100として100自由度モデルのモデルで説明したいと思います。
ここでは、「モード解析」を説明する前段階（準備）として、質量行列と剛性行列を作成するプログラムを紹介します。ちなみに、私の愛読している長松先生著の”モード解析入門”を参考にしています。

 

理論

　　質量行列

質量行列Mは下のようになります。

　　剛性行列

剛性行列Kは下のようになります。

スポンサーリンク

プログラム

教科書では質量行列や剛性行列の要素（m1やm2、k1やk2など）を全て同値のmやkとして、単純化して解くことが多いですが、本プログラムでは先々のことを考えて汎用的に作ります。
下記のm_vecおよびk_vecは、下式を意味します。

　　質量行列

function [M]=eval_Mmatrix(m_vec)

M=diag(m_vec);

end

 

　　剛性行列

function [K]=eval_Kmatrix(k_vec)

K=zeros(length(k_vec));
for ii1=1:length(k_vec)
    if ii1==1
        K(ii1,ii1)=k_vec(ii1);
    else
        K(ii1-1:ii1,ii1-1:ii1)=K(ii1-1:ii1,ii1-1:ii1)+[1 -1;-1 1]*k_vec(ii1);
    end
end

end

結果

試しにm_vecとk_vecを適当に入力して、動作を確認してみました。正しく動いていることがわかります。

スポンサーリンク

今回はこのへんでGood luck