MATLABで学ぶ振動工学質量付加を利用した構造最適化 - MATLABパイセンが教える振動・騒音・音響・機械工学

はじめに
（初級編）構造最適化の概要
MATLABプログラム
1. 関連

はじめに

今回は「構造最適化」について説明します。構造最適化の手法はいろいろありますが、下記記事で説明した「質量付加による伝達関数の変化」の予測式を用いることにします。

MATLABで学ぶ振動工学　質量付加による伝達関数の変化

質量付加による伝達関数の変化は理論式で予測することができます。本記事ではその理論式を紹介し、その精度をバネマス系で検証しました。

この予測式を使うと、実測のFRFだけを使って付加質量による変化を予測することができます。更に、この予測式を発展させることで実測のFRF結果だけを使って、振動を低減する方向性を理解することができます。

（初級編）構造最適化の概要

（復習）質量付加による伝達関数の変化

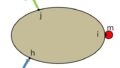
構造体の点iに質量mが付加されたとき、力Fが作用している点hと点j間の伝達関数newGjhは質量付加前の伝達関数Gjhで表すことができる。

$$
newG_{jh}=G_{jh}-\frac{G_{ji}G_{ih}}{G_{ii}-\frac{1}{ω^2 m}}
$$

図1　質量付加による伝達関数の変化

構造最適化への入り口

最適化問題で値を変更しても良い変数を「設計変数」と呼びます。下図の付加質量mを変更してよい場合、mが設計変数となります。

ちなみに、本記事では下記の例題で議論を進めたいと思います。

○例題
図1のような4自由度のバネマス系でm2に力Fが作用し、付加質量mはどこに付加して良いとします。このmは複数の位置に付加してもいいとします。このときの質量付加前後の伝達関数G_4,2を求めなさい。ここで、質量はm1=m2=m3=m4=1 [kg] 、バネ定数はk1=k2=k3=k4=10^3とする。

図2　例題

では、上記の例題で変位振動X4を最小化するにはmをどうすればいいでしょうか？
このように漠然とした質問を投げかけると、賢い人であれば下記のように疑問を持ちますよね？

それって、mの変化範囲や、変位振動X4を最小化したい周波数や周波数帯域によって変わるのではないですか？

その疑問は正解です。このままでは、”最小”の定義が曖昧なので解けません。

なので、とりあえず下記のような条件を加えたいと思います。
○条件
2.2Hzにおける変位振動X4が最小となる付加質量mの値を求める。ただし、付加質量mの合計値の範囲は-0.9<m<2 [kg]

みなさんはどうやってアプローチしますか？
学生さんなどは下記のように考える人が多いのではないでしょうか？

newGの式を使って、5Hzのときの各Gを使って、全パターン求めて最小の付加質量mを求めよう！

悪くない手だと思いますが、組み合わせが膨大なので、全組み合わせを計算するのは無理ですよね。
また、「その結果が本当に”最小”なのですか？0.00001kgぐらい変えたらもっと良くなったりしないの？」と質問されたときに、「いいえ、私の結果が”最小”です」と断言できないと思います。（検討してみた中で最も低かっただけかと思います。）

「”最小”です」と断言するには、論理的な説明が必要になります。

御託はこの辺にして、解法の説明をしたいと思います。まず、質量付加する前の伝達関数G_jhの付加質量mに対する感度を求めます。ただし、直接的に求められないので、冒頭で示した質量付加後の伝達関数newG_jhの式から求めます。

質量付加後の伝達関数newG_jhの付加質量mに対する感度は、伝達関数newG_jhを付加質量mの偏微分で表されます。従って以下になります。

$$
\frac{\partial newG_{jh}}{\partial m} = \frac{G_{ji}G_{ih}}{ω^2(m G_{ii}-\frac{1}{ω^2} )^2}
$$

このmが微小のとき（mが0に近いとき）が”伝達関数G_jhの付加質量mに対する感度”なので、以下で表現できます。

$$
\frac{\partial G_{jh}}{\partial m} = ω^2 G_{ji} G_{ih}
$$

さらに、mが微小のときはG_{jh}をテイラー展開して、1次までを考慮した近似式で予測できますよね。従って下式が成立します。

$$
newG_{jh} =G_{jh} + \frac{\partial G_{jh}}{\partial m} dm
$$

微小な付加質量dmを少しずつ変化させて、最終的に-0.9<m<1の範囲で変化させるイメージです。

ちなみに、感度についてですが、感度が高ければ、質量mを付加することで伝達関数G_jhを大きく変化させることができます。一方、感度が低ければ、質量mを付加しても伝達関数G_jhは変化しません。

従って、感度が高いところに質量mを付加する必要があります。ただし、感度は正負がありますが、伝達関数Gは複素数なので、正なのか負なのかよくわかりません。そこがやっかいなところです。

MATLABプログラム

結果

先に結果を図3に示します。黒線が最適化前、赤線が最適化後です。2.2Hzの応答が小さくなっているのがわかります。

図3　最適化結果

ちなみに、dm=0.001で解くと、m1=1,m2=1.001,m3=1,m4=2.999となりました。

今回は”質量付加”なので簡単に解くことができました。しかし、バネ定数kが設計変数の場合やmとkの両方が設計変数の場合は、最適化で使用する理論式が全然違います。
次回はその辺について説明したいと思います。

今日はこのへんでGood luck!

コード

clear all
close all
% % % % 初期設定
k_vec=[1 1 1 1]*10^3;
[K]=eval_Kmatrix(k_vec);
freq=0.5:0.1:20;
f=[0;1;0;0];
C=zeros(length(k_vec));

% % % % 質量付加前の質量行列
m_vec=[1 1 1 1];
[M]=eval_Mmatrix(m_vec);
before_x=eval_direct_x(M,K,C,f,freq);
% % % % % % 
figure(1)
loglog(freq,abs(before_x(4,:)),'k') %力fの成分が1なので、xを伝達関数Gは同じになるのでxを表示
hold on

% % % % % % 感度の算出
G_2i_5Hz=eval_direct_x(M,K,C,f,5); %ややこしいので再計算
G_i4_5Hz=eval_direct_x(M,K,C,[0;0;0;1],5); %Gih　相反定理

dGdm=(2*pi*5)^2*G_2i_5Hz.*G_i4_5Hz;

% % % % % % 最小化問題
% m=[-0.9 2]

% % % % % % 質量付加後の質量行列
vec=[1 1 1 1];
dm=0.001; %微小な質量
target_f=2.2;
while sum(vec)&amp;amp;amp;lt;6 &amp;amp;amp;amp;&amp;amp;amp;amp; sum(vec)&amp;amp;amp;gt;4-0.9 
    [tempdGdm,id]=sort(abs(dGdm),'descend');
if id(1)==1
    m_vec1=vec+[dm 0 0 0];
    m_vec2=vec+[-dm 0 0 0];
elseif id(1)==2
    m_vec1=vec+[0 dm 0 0];
    m_vec2=vec+[0 -dm 0 0];
elseif id(1)==3
    m_vec1=vec+[0 0 dm 0];
    m_vec2=vec+[0 0 -dm 0];
elseif id(1)==4
    m_vec1=vec+[0 0 0 dm];
    m_vec2=vec+[0 0 0 -dm];
else
    error('なにかおかしい')
end

[M1]=eval_Mmatrix(m_vec1);
[M2]=eval_Mmatrix(m_vec2);

after_x1=eval_direct_x(M1,K,C,f,target_f);
after_x2=eval_direct_x(M2,K,C,f,target_f);

if abs(after_x1(4)) &amp;amp;amp;lt; abs(after_x2(4))
    if sum(m_vec1) &amp;amp;amp;gt;=6 || sum(m_vec1) &amp;amp;amp;lt;=4-0.9 
        break
    end
    vec=m_vec1;
    M=M1;
else
    if sum(m_vec2) &amp;amp;amp;gt;=6 || sum(m_vec2) &amp;amp;amp;lt;=4-0.9 
        break
    end
    vec=m_vec2;
    M=M2;
end
if sum(vec) &amp;amp;amp;gt;=6 || sum(vec) &amp;amp;amp;lt;=4-0.9 
    break
end
% % % % % % 感度の再計算
G_2i_5Hz=eval_direct_x(M,K,C,f,target_f); %
G_i4_5Hz=eval_direct_x(M,K,C,[0;0;0;1],target_f); %Gih　相反定理
dGdm=(2*pi*5)^2*G_2i_5Hz.*G_i4_5Hz;
end

after_x=eval_direct_x(M,K,C,f,freq);
% % % % % % 
figure(1)
loglog(freq,abs(after_x(4,:)),'r')
loglog([target_f target_f],[10^-5 10^0],'b--')
xlim([freq(1) freq(end)])
sum(vec)

○functionファイル

function [M]=eval_Mmatrix(m_vec)
M=diag(m_vec);
end

function [K]=eval_Kmatrix(k_vec)
K=zeros(length(k_vec)); 
for ii1=1:length(k_vec) 
    if ii1==1 K(ii1,ii1)=k_vec(ii1); 
    else 
        K(ii1-1:ii1,ii1-1:ii1)=K(ii1-1:ii1,ii1-1:ii1)+[1 -1;-1 1]*k_vec(ii1);
    end
end

end

function x=eval_direct_x(M,K,C,f,freq)

x=zeros(length(f),length(freq));
j=sqrt(-1);
for ii1=1:1:length(freq)
    w=2*pi*freq(ii1);
    x(:,ii1)=inv(K+j*w*C-w^2*M)*f;
end

end