はじめに
昨日、下記記事を書きました。
MATLAB で学ぶ信号処理 チャープ信号を畳み込むとどうなる？
チャープ信号とチャープ信号を反転させた信号を畳み込み積分するとインパルス信号になります。
mech-eng-uni.com
2021.09.13
加振試験を行うときに、チャープ信号（スイープ信号）とインパルス信号のいずれでも加振することができますが、チャープ信号が多く使われている理由がわかりますか？
ほとんどの方はご存じだとは思いますが、知らない人のために、念のためですが説明しておきます。
加振機やスピーカーの構造
下図でスピーカー駆動の可動域について説明します。
図に示すように、スピーカーではエッジでコーンを結合してますので、エッジによって可動域に制約があります。これは加振機でも同様の制約があります。
図では、インパルス波を入力すると、波形の振幅は最大でAmaxまでしか取り柄ません。
時刻歴波形の振幅がAmaxまでとなってしまうとどのような問題があると思いますか？
MATLABで示しながら説明したいと思います。
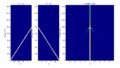
Amax=5として、チャープ信号信号とインパルス信号の時間波形を下図で比較します。
パッと見で、1秒間のエネルギーはどっちが大きそうですか？
圧倒的にチャープ信号の方が大きそうですよね？（積算の振幅が大きいので、エネルギーが大きそうだな―と簡単に想像がつく）
では、実際にFFTをして、各周波数の振幅がどうなっているのかを見てみましょう。FFT結果が下図です。
インパルス波よりもチャープ信号の方が単位周波数の振幅が大きいですよね。
もし、暗騒音が大きい場合やノイズ成分が大きい場合、インパルス信号ではSNが非常に悪くなってしまいます。一方、チャープ信号ではSNが改善された応答信号を取得できます。
MATLABコード
clear all;close all
fs=1024*4;
t=0:1/fs:1;
t=t(1:fs);
Amax=5;
y1 = Amax*chirp(t,10,1,1000,'linear', -90); %チャープ信号
imp=zeros(1,length(t));
imp(2)=Amax; %インパルス信号
figure
plot(t,y1)
hold on
plot(t,imp,'r')
xlabel('時間 [s]')
ylabel('振幅')
Y1=fft(y1,fs);
Imp=fft(imp,fs);
figure
subplot(211)
semilogy(0:fs-1,abs(Y1))
hold on
semilogy(0:fs-1,abs(Imp),'r')
xlabel('周波数 [Hz]')
ylabel('振幅')
subplot(212)
plot(0:fs-1,angle(Y1))
hold on
plot(0:fs-1,angle(Imp),'r')
xlabel('周波数 [Hz]')
ylabel('位相')
コメント