はじめに
ドラゴンクエストのテリーのワンダーランドでは、
スライム+5♂ と スライム+5♀
を配合するとキングスライムができます。
これと同様に、チャープ信号♂とチャープ信号♀を畳み込み積分するとインパルス波形になります。
「えっ??なんでー?」って疑問に思った方はおそらく、チャープ信号(サインスイープ信号やTSPとも呼ぶ)というものを理解していませんし、逆FFTや畳み込み積分についても理解できていません。
本記事では、チャープ信号の理解が不足していそうな点だけざっくりと説明します。
チャープ信号とチャープ信号の畳み込み
MATLABによる検証
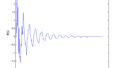
下図のようにチャープ信号(スイープ①とスイープ②)を畳み込み積分すると、インパルス応答になっていることがわかりますね。
MATLABのコード
clear all;close all
fs=1024*8*4;
t=0:1/fs:1;
% t=t(1:fs);
y1 = chirp(t,10,1,10000,'linear', -90);
y2=y1(end:-1:1);
figure
subplot(211)
plot(t,y1)
subplot(212)
plot(t,y2)
sig=conv(y1,y2);
figure
plot(sig)
figure
subplot(141)
spectrogram(y1,1024,1024/2,1024,fs)
view([90 -90])
caxis([-70 -20])
title('スイープ①')
subplot(142)
spectrogram(y2,1024,1024/2,1024,fs)
view([90 -90])
caxis([-70 -20])
title('スイープ②')
subplot(1,4,3:4)
spectrogram(sig,1024,1024/2,1024,fs)
view([90 -90])
caxis([-30 10])
title('①②の畳み込み積分')
チャープ信号の考え方
みなさんチャープ信号はご存じかと思います。下図のような、時々刻々と周波数が変化する正弦波のような信号ですね。
この信号をFFTしてみます。
ただ、上記信号の1s付近の拡大図を先に紹介しておきます。
上図に示すように1s付近がきれいに0になってませんね。。。。なので、FFTすると変なノイズがのってしまいますが、ご了承ください。
FFTの結果が下記です。
今回のチャープ信号はfs=4096で、下記のように作成しています。
y1 = chirp(t,10,1,1000,'linear', -90); Y1=fft(y1,fs);
従って、周波数成分は10~1000Hzしか存在しません。
FFTの結果からわかることは、10~1000Hzで振幅がフラットであることです。
もう少しわかりやすく説明するために、200Hzまでの拡大図を示します。
振幅が(ほぼ)フラットで、位相が線形的に遅れていることがわかりますね。そのため、インパルス信号に位相成分を持たせて、時間軸上に引き延ばした信号がチャープ信号という考え方ができますね。
今日はここらへんで、やめておきます。
後日もう少しディープな世界の話をしたいと思います。

コメント