はじめに
音場制御とは文字通り、音場を制御(コントロール)することです。一般的に、音場を制御するためにスピーカーを使用します。みなさんも聞いたことがあると思いますが、音は音で打ち消すことができます。
例えば、ノイズキャンセリングイヤホンなんかも、イヤホンの外側にあるマイクで外部の音を計測して、鼓膜に届く音を予測し、その音を打ち消す音をイヤホンから出力することで、人間の耳では外部音が聞こえず、イヤホンからのクリアな音だけが聞こえるようになります。
これを部屋のような大きな空間で実施するのが、本ブログで取り上げる音場制御です。
(夢がありますよねー)
フィードフォワード制御とフィードバック制御
まず、音場制御にはフィードフォワード制御とフィードバック制御があります。
フィードバック制御は、文字通りフィードバックをしながら制御する方法です。
例えば、エアコンや冷蔵庫の温度調整などがあげられます。リモコンで26℃に設定して電源をONにすると、徐々に部屋の温度が26℃に近づきます。26℃に近づいているかを赤外線センサーなどでモニタリング(フィードバック)をしつつ、26℃に近づいたときには、冷却を弱めるような運転モードに切り替わります。このようにセンサーでフィードバックを取りながら制御する方法をフィードバック制御と呼びます。
一方、フィードバックを取らない制御をフィードフォワード制御と呼びます。
本ブログではフィードフォワード制御を取り上げます。(フィードバック制御は制御理論が絡むので、音響工学よりも制御工学の要素が強く、私ではうまく説明できません。)
音場制御のイメージ
音場制御のイメージを図1に示します。図1(a)に示すように空間にスピーカーを配置します。ここではスピーカーは壁に設置する形になっていますが、空間内にあっても問題ありません。これらの各スピーカーに対してフィルタリング処理をすることで、図1(b)のような赤い空間と青い空間を作り出します。例えば、赤い空間では音楽が聞こえますが、青い空間では無音(静か)な空間というように別々の音環境を構成することができます。この図では赤と青の2つの空間を作っていますが2つ以上を作り出すこともできます。

(a) スピーカーと空間

(b) 各音場のイメージ
図1 音場制御のイメージ
スポンサーリンク
音場制御の理論
基本的な理論は(おそらく)高校生の数学で十分です。
まず、工学というのは(ほとんど)線形の学問です。流体力学などでは非線形も扱いますが、振動・音響・機械工学では線形システムとみなして考えるのが一般的です。(研究者の中には非線形で解くことで論文を書いてる人がたくさんいますが、機械工学(mechanical engineering)とはそもそも”実用的な学問”なので、非実用的な非線形で解くというのはナンセンスだと個人的には思います。圧倒的なメリットがあるなら別ですが…)
線形システムでは図2のような関係が成り立ちます。図2に示すように応答pは入力qに伝達関数Gを乗じた形で表せます。中学校で習うフックの法則のようなものです。力Fはバネ定数kとxの関係で下式のように表しますよね。それと同じです。
$$ F = kx $$

図2 線形システムの関係
ただし、スピーカー1個でマイクが2本ある場合は、図3のようになります。
 図3 線形システムの関係2
図3 線形システムの関係2
では、スピーカーn個でマイクがm本の場合は?と考えます。ここで便利なのが行列です。”線形代数”とはそういう意味なのか!と学生ながら納得したものです。
\(
\left(
\begin{array}{c}
p_1 \\
\vdots \\
p_m
\end{array}
\right)= \begin{pmatrix}
G_{11} & \cdots & G_{1n} \\
\vdots & \ddots & \vdots \\
G_{m1} & \cdots & G_{mn}
\end{pmatrix}
\left(
\begin{array}{c}
q_1 \\
\vdots \\
q_n
\end{array}
\right)
\)
ここまで理解できればほぼ音場制御の大枠は理解したことになります。
音場制御の理論(音場再構成の方法)
先ほど下式でほぼ音場制御が理解できたものだと述べました。
\(
\left(
\begin{array}{c}
p_1 \\
\vdots \\
p_m
\end{array}
\right)= \begin{pmatrix}
G_{11} & \cdots & G_{1n} \\
\vdots & \ddots & \vdots \\
G_{m1} & \cdots & G_{mn}
\end{pmatrix}
\left(
\begin{array}{c}
q_1 \\
\vdots \\
q_n
\end{array}
\right)
\)
学生から「いやいや、これだけじゃ音場制御は無理っしょ!」と言われそうですね。
なので、もう少し詳しく説明します。図1の赤と青の別々の音場を作るためには、図4の左上の「赤い空間だけ音源1が聞こえ、もう一方の空間には音が聞こえない」という解(フィルター)と、右上の「青い空間だけ音源2が聞こえ、もう一方の空間には音が聞こえない」という解(フィルター)の両方を求めます。そして、各スピーカーにフィルタリングした音源1を流します。更に、各スピーカーにフィルタリングした音源2を流します。すると、図4の下のように赤と青の別々の空間が構成できます。
 図4 各音場の制御方法
図4 各音場の制御方法
「では、このフィルターはどうやって作成するのですか?」と質問されそうですね。
それは各スピーカーのフィルターはqになります。ただし、このフィルターqは目標音場p_targetを構成できるqを指します。
\(
\left(
\begin{array}{c}
q_1 \\
\vdots \\
q_n
\end{array}
\right)= \begin{pmatrix}
G_{11} & \cdots & G_{1n} \\
\vdots & \ddots & \vdots \\
G_{m1} & \cdots & G_{mn}
\end{pmatrix} ^{\mathrm{-1}}
\left(
\begin{array}{c}
p_{target1} \\
\vdots \\
p_{targetm}
\end{array}
\right)
\)
もっと具体的に説明すると、音の聞こえる方の音場をブライトゾーン、音の聞こえない方の音場をダークゾーンと呼びます。それどれのゾーン毎に目標応答p_targetと伝達関数行列Gを分けて表すと下式のようになります。このときのqは、目標応答q_targetを満たす入力音源の相対的な位相差と振幅比を求めていることになります。このqを再生したい音源に対してフィルタリング処理することで、各スピーカーに相対的な位相差と振幅比を再現することができます。
\(
\left(
\begin{array}{c}
q_1 \\
\vdots \\
q_n
\end{array}
\right)= \begin{pmatrix}
G_{bright} \\
G_{dark}
\end{pmatrix} ^{\mathrm{-1}}
\left(
\begin{array}{c}
p_{target bright} \\
p_{target dark}
\end{array}
\right)
\)
 図5 ブライトゾーンとダークゾーンの説明
図5 ブライトゾーンとダークゾーンの説明
MATLABでの検証
では、プログラムを組んで理論を検証しましょう。
ここでは入力-応答間の伝達関数を球面波で求めることにします。過去に球面波のプログラム方法について説明しているので、よかったらそちらも確認ください。

スポンサーリンク

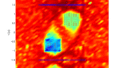
先にプログラムでの検証結果を図6に示します。
- 音源の位置は、青丸で示したy軸±1.5m
- ブライトゾーンは、x軸0.1~0.7mでy軸0.4~1.0mのゾーン
- ダークゾーンは、x軸-0.7~-0.1mでy軸-1.0~-0.4mのゾーン


図6 音場制御の検証結果
どう思いますか?
確かに2つのゾーンに分かれており、ダークゾーンは音圧が低くなっています。
しかしブライトゾーンは、ブライトゾーン以外のところよりも音圧が低いですね。
音場制御では目標音場pを設定していないエリアの音場は考慮されていないので、どのような音場になるかわからないのです。
もし、ブライトゾーン以外は音圧を低くしたい場合は、ブライトゾーン以外の全てのエリアをダークゾーンとして計算する必要があります。図6のブライトゾーンとダークゾーンだけを比較すると、2つの異なる音場を構成することができたと言えますね。
このフィードフォワードの音場制御理論は、本記事で紹介した単純な逆行列計算よりも最適化計算をすることで、より効率的に音場制御ができます。
次回からは”音場制御の最適化”について説明したいと思います。
今回はこのへんでGood luck
スポンサーリンク
clear all;close all;clc
% % % % % % 初期設定
x=-2:0.1:2;
y=-2:0.1:2;
rho=1.293;
A=1;
c=340; %音速
freq=5000; %周波数
w=2*pi*freq;
k=w/c;
% % % % % % 音源位置の設定
x_sp=-1:0.02:1;
y_sp=ones(1,length(x_sp));
input=[x_sp x_sp
y_sp*(-1.5) y_sp*(+1.5)].';
% % % % % % ブライトゾーンとダークゾーンの設定
bz_geo=[];
dz_geo=[];
bz_x=-0.3:0.1:0.3;
bz_y=-0.3:0.1:0.3;
for ii1=1:length(bz_x)
for ii2=1:length(bz_y)
bz_geo=[bz_geo;bz_x(ii1)+0.4 bz_y(ii2)+0.7];
dz_geo=[dz_geo;bz_x(ii1)-0.4 bz_y(ii2)-0.7];
end
end
zone=[bz_geo;dz_geo];
Gb=zeros(size(bz_geo,1),size(input,1));
Gd=zeros(size(dz_geo,1),size(input,1));
for ii1=1:size(bz_geo,1)
for ii2=1:size(input,1)
r_bz=sqrt( (bz_geo(ii1,1)-input(ii2,1))^2 + (bz_geo(ii1,2)-input(ii2,2))^2 );
r_dz=sqrt( (dz_geo(ii1,1)-input(ii2,1))^2 + (dz_geo(ii1,2)-input(ii2,2))^2 );
if r_bz<0.1
r_bz=0.1; %r=0の時にP(ii1,ii2)が無限大になるのを防ぐ目的
end
if r_dz<0.1
r_dz=0.1; %r=0の時にP(ii1,ii2)が無限大になるのを防ぐ目的
end
Gb(ii1,ii2)=j*w*rho*A./(4*pi*r_bz).*exp(j*(k*r_bz));
Gd(ii1,ii2)=j*w*rho*A./(4*pi*r_dz).*exp(j*(k*r_dz));
end
end
G=[Gb;Gd];
p=[ones(size(Gb,1),1);zeros(size(Gd,1),1)];
q=pinv(G)*p;
P=zeros(length(y),length(x));
for ii1=1:length(x)
for ii2=1:length(y)
for ii3=1:size(input,1)
r=sqrt( (x(ii1)-input(ii3,1))^2 + (y(ii2)-input(ii3,2))^2 );
if r<0.2
r=0.2; %r=0の時にP(ii1,ii2)が無限大になるのを防ぐ目的
end
P(ii2,ii1)=P(ii2,ii1)+q(ii3)*j*w*rho*A./(4*pi*r).*exp(j*(k*r));
end
end
end
% x(ii1)およびy(ii2)という位置における振幅abs(P(ii1,ii2))は一意に決まるため
% P(ii1,ii2)を複素数平面上で回転させれば、音波が伝搬するアニメーションが作成できる
% figure(1)
% surf(x,y,abs(P))
% shading interp
% ylabel('X [m]')
% xlabel('Y [m]')
t=linspace(0,2*pi,6)/w;
for ii1=1:length(t)
clf
% surf(x,y,real( P*exp(j*(-w*t(ii1))) ))
surf(x,y,log10(abs(real( P*exp(j*(-w*t(ii1))))) ))
shading interp
hold on
plot3(input(:,1),input(:,2),ones(size(input,1),1)*50,'o')
plot3(zone(:,1),zone(:,2),ones(size(zone,1),1)*50,'ro')
ylabel('Y [m]')
xlabel('X [m]')
view([0 90])
% pause(0.1)
saveas(gcf,[num2str(ii1+100) '.png'],'png')
end


コメント