MATLABで学ぶ信号処理【完全版】振動・騒音のfftおよびオートパワーのプログラム

はじめに
おさらい（振幅と実効値）
窓関数の補正
MATLABプログラム
おまけ（窓関数の補正係数の導出）
1. 関連

はじめに

これまでにfftやオートパワー、窓関数についての記事を書きました。
それらの記事をまとめつつ、みなさんの使い勝手の良いfunctionファイルを提供しようと思います。
過去の記事の繰り返しになりますが、MATLABのfft関数だけでは、振動騒音の周波数分析結果（スペクトル）とは一致しません。

○過去記事はこちら↓

MATLABで学ぶ信号処理　窓関数について

fttと窓関数の関係についてざっくりと説明します。ざっくりなので、専門家には指摘したい箇所があると思いますが、実用上は下記の理解で困らないと思うので、大目に見てください。

MATLABで学ぶ信号処理　窓関数処理後の振幅とパワーについて1

本記事では、窓処理がfft結果の振幅やパワースペクトルに及ぼす影響について説明します。また、振幅とパワースペクトルの関係について詳しく説明します。

MATLABで学ぶ信号処理　窓関数処理後の振幅とパワーについて2

市販のFFTアナライザや計測器で計測したスペクトルやオートパワー、オクターブの結果と、自作のMATLABやPythonプログラムで時刻歴波形から計算したスペクトルやオートパワー、オクターブが一致しないことがあります。それは、窓関数による振幅やエネルギーの補正が間違っているか、使い分けができていないことが原因です。この記事では窓関数の補正について詳しく述べています。小野測器のDSシリーズ、シーメンスのScadas、Brüel & KjærのPulseなどの計測器を使用していると考えられます。その計測器でオートパワーもしくはスペクトルを計測している。また、オクターブ結果やO.A.結果も測定・計算している、ということだと思います。そして、計測器で測定・計算したオクターブ結果やO.A.結果と、自分でオートパワーから計算したオクターブ結果やO.A.結果が一致しない、ということで質問してきたのだと思われます。

詳細情報をお探しの方は下記文献が参考になると思います。

<br />

おさらい（振幅と実効値）

下図のような振幅Aの時間信号があります。これをfftしてスペクトルを求めたい場合、振幅Aを求めるのか、振幅の実効値を求めるのかのを明確にしておく必要があります。一般的に、振動や騒音は”実効値”で評価で評価することになります。

図1　信号

ここで振幅Aを求めることを”peak”と呼び、実効値を求めることを”RMS”と呼ぶことにします。
すると、下記のようにまとめることができます。

表1　比較表

	peak	RMS
スペクトル	A	A/√2
オートパワー	A^2	A^2/2
PSD	A^2/df	A^2/2/df

（詳しく説明しませんが、PSDも比較表に載せました）

ここまでは問題ないですよね。

窓関数の補正

次に、窓関数を使った場合の補正について説明します。詳細な説明は下記をご確認ください。

MATLABで学ぶ信号処理　窓関数処理後の振幅とパワーについて1

窓関数の種類によって補正係数が変わります。

表2　窓関数の補正係数

	レクタンギュラ窓 (rectangular)	ハニング窓 (hanning)	ハミング窓 (hamming)	ブラックマン窓 (blackman)
スペクトル	1	1/0.5	1/0.54	1/0.42
オートパワー (周波数特性用)	1^2	(1/0.5 )^2	( 1/0.54 )^2	( 1/0.42 )^2
オートパワー (帯域計算用)	1	8/3	(50^22/(27^22+23^2)	(25^22^3)/(21^22+25^2+2^2)
PSD	1	8/3	(50^22/(27^22+23^2)	(25^22^3)/(21^22+25^2+2^2)

MATLABプログラム

結果（functionファイルの動作確認）

先にfunctionファイルの動作確認結果を示します。

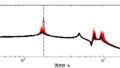
図2　スペクトラム

図3　オートパワー

図3のオーパワーの結果では振幅値がレクタンギュラ窓とハニング窓で違いますが、ハニング窓では999Hzや1001Hzに成分（振幅値）を持っています。ハニング窓の999Hz～1001Hzの振幅値を足すと、レクタンギュラ窓の振幅値と一致します。つまり、O.A値やオクターブ分析結果が一致するように補正をしていることになります。

実行コード（functionファイルの動作確認用）

clear all;clc;close all

fs=1024*4;
t=linspace(0,1,fs+1);
sig=sin(2*pi*1000*t);
[freq,fft_coe,peak_fftdata,RMS_fftdata]=fft4Spectrum(sig,fs,fs,'rectangular');
[freq,fft_coe,peak_power,RMS_power]=fft4Power(sig,fs,fs,'rectangular');
figure(1)
subplot(211)
plot(freq,abs(peak_fftdata))
hold on
plot(freq,abs(RMS_fftdata),'r')
legend('振幅','RMS')
xlim([990 1010])
title('窓関数なし（rectangular窓）')

figure(2)
subplot(211)
plot(freq,abs(peak_power))
hold on
plot(freq,abs(RMS_power),'r')
legend('振幅','RMS')
xlim([990 1010])
title('窓関数なし（rectangular窓）')


[freq,fft_coe,peak_fftdata,RMS_fftdata]=fft4Spectrum(sig,fs,fs,'hanning');
[freq,fft_coe,peak_power,RMS_power]=fft4Power(sig,fs,fs,'hanning');
figure(1)
subplot(212)
plot(freq,abs(peak_fftdata))
hold on
plot(freq,abs(RMS_fftdata),'r')
legend('振幅','RMS')
xlim([990 1010])
title('hanning窓')

figure(2)
subplot(212)
plot(freq,abs(peak_power))
hold on
plot(freq,abs(RMS_power),'r')
legend('振幅','RMS')
xlim([990 1010])
title('hanning窓')

functionファイル

スペクトル（fft for spectrum）

function [freq,fft_coe,peak_fftdata,RMS_fftdata]=fft4Spectrum(sig,fs,N,window)
% % % % input
% sig   : 時刻歴信号
% N     : fftのデータ数（Line数）
% fs    : サンプリング周波数
% window: 窓関数名（レクタンギュラ窓、ハニング窓、ハミング窓、ブラックマン窓が使用可能）
% 
% % % % output
% freq    :周波数
% fft_coe :窓関数の補正係数
% peak_fftdata :時間信号の振幅を求めたい場合に使用
% RMS_fftdata  :実効値のfft結果（通常、振動騒音ではこれを使う）
% 
% ★注意
% -------パワーを計算したい場合は下記計算をすること-------
% peak_fftdata.^2/fft_coe(1)^2*fft_coe(2)
% RMS_fftdata.^2/fft_coe(1)^2*fft_coe(2)

% size(sig)は(1,length(sig))となるようにしたいので、ここでチェック
if size(sig,1)==length(sig)
    sig=sig.';
end
[win,fft_coe]=get_window(length(sig),window);
fftdata=fft(sig.*win,N)/N;

freq=linspace(0,fs/2,floor(N/2)+1);
% % % peak(時間信号の振幅を求めたいとき)
peak_fftdata=fftdata(1:floor(N/2)+1)*2*fft_coe(1); %負の周波数分の補正

% % % RMS(実効値)
RMS_fftdata=peak_fftdata/sqrt(2);

end


function [win,fft_coe]=get_window(N,window)
t=linspace(0,1,N);
switch window
    case 'rectangular'
        win = ones(1,N);
        fft_coe=[1 1];
    case 'hanning'
        win = 0.5*ones(1,N) - 0.5*cos(2.0*pi*t);        
        fft_coe=[2 8/3];
    case 'hamming'
        win = 0.54*ones(1,N) - 0.46*cos(2.0*pi*t);
        fft_coe=[1/0.54 1/( (27^2*2+23^2)/(50^2*2) )];
    case 'blackman'
        win = 0.42*ones(1,N) - 0.5*cos(2.0*pi*t) + 0.08*cos(4.0*pi*t);
        fft_coe=[1/0.42 1/( (21^2*2+25^2+2^2)/(25^2*2^3) )];
end

end

帯域計算用オートパワー（fft for power）
これは、O.A.値やオクターブ分析などの帯域のパワーを計算するときに使う。

function [freq,fft_coe,peak_fftdata,RMS_fftdata]=fft4Power(sig,fs,N,window)
% % % % input
% sig   : 時刻歴信号
% N     : fftのデータ数（Line数）
% fs    : サンプリング周波数
% window: 窓関数名（レクタンギュラ窓、ハニング窓、ハミング窓、ブラックマン窓が使用可能）
% 
% % % % output
% freq    :周波数
% fft_coe :窓関数の補正係数
% peak_fftdata :時間信号の振幅を求めたい場合に使用
% RMS_fftdata  :実効値のfft結果（通常、振動騒音ではこれを使う）
% 

% size(sig)は(1,length(sig))となるようにしたいので、ここでチェック
if size(sig,1)==length(sig)
    sig=sig.';
end
[win,fft_coe]=get_window(length(sig),window);
fftdata=fft(sig.*win,N)/N;

freq=linspace(0,fs/2,floor(N/2)+1);
fftdata=fftdata(1:floor(N/2)+1)*2; %負の周波数分の補正
% % % peak(時間信号の振幅を求めたいとき)
peak_fftdata=fftdata.^2*fft_coe(2);

% % % RMS(実効値)
RMS_fftdata=peak_fftdata/2;

end


function [win,fft_coe]=get_window(N,window)
t=linspace(0,1,N);
switch window
    case 'rectangular'
        win = ones(1,N);
        fft_coe=[1 1];
    case 'hanning'
        win = 0.5*ones(1,N) - 0.5*cos(2.0*pi*t);        
        fft_coe=[2 8/3];
    case 'hamming'
        win = 0.54*ones(1,N) - 0.46*cos(2.0*pi*t);
        fft_coe=[1/0.54 1/( (27^2*2+23^2)/(50^2*2) )];
    case 'blackman'
        win = 0.42*ones(1,N) - 0.5*cos(2.0*pi*t) + 0.08*cos(4.0*pi*t);
        fft_coe=[1/0.42 1/( (21^2*2+25^2+2^2)/(25^2*2^3) )];
end

end